Regelungssysteme
(EN google-translate)
(PL google-translate)
ALL SOFTWARE ON www.kramann.info IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
Sommersemester 2017
Verbindliche Folienvorlage zum Tag der offenen Tür 19.5.2017
 folienvorlage.zip - Verbindliche Folienvorlage zum Tag der offenen Tür 19.5.2017
folienvorlage.zip - Verbindliche Folienvorlage zum Tag der offenen Tür 19.5.2017
 geregelter_schwinger.zip - Linearer Schwinger mit P, D und PD-Regler
geregelter_schwinger.zip - Linearer Schwinger mit P, D und PD-Regler
 zieglernichols1.zip - 1.Methode nach Ziegler und Nichols.
zieglernichols1.zip - 1.Methode nach Ziegler und Nichols.
 identifikation.zip
identifikation.zip
 identifikation2.zip
identifikation2.zip
Material für die Lenkregelung der Elektrokutsche
VIDEO Kutsche geschoben bei aktiver P-Lenkregelung, 19.04.2017.
VIDEO Kutsche selbstfahrend mit P-Lenkregelung, 19.04.2017.
VIDEO Kutsche, Kreisfahrt mit P-Lenkregelung und "Totmanntaster", 09.05.2017.

Bild 0-1: Kutsche von hinten. Man sieht die Motortreiber. Der Koffer enthält die Lithiumbatterien.

Bild 0-2: Kutsche von vorne. Man sieht die auf den Boden gerichtete USB-Kamera für die Linienverfolgung.
 MotorAnsteuernSerial33-85.zip - Arduino-Micro-Programm zur Ansteuerung der Brushless-Motoren.
MotorAnsteuernSerial33-85.zip - Arduino-Micro-Programm zur Ansteuerung der Brushless-Motoren.
 K1_seriell.zip - Serielle Ansteuerung des Arduino Micro (PWM-Geber) mit Processing.
K1_seriell.zip - Serielle Ansteuerung des Arduino Micro (PWM-Geber) mit Processing.
 K2_cam.zip - Ansteuern einer USB-Kamera mit Processing und Auslesen der Farbwerte.
K2_cam.zip - Ansteuern einer USB-Kamera mit Processing und Auslesen der Farbwerte.
 K3_cam.zip - Extrahieren des Rotanteils.
K3_cam.zip - Extrahieren des Rotanteils.
 K3_cam_Hoch.zip - Schwerpunktpildung und Berechnung der Regeldifferenz (Eric Hoch, Masterstudent CARE)
K3_cam_Hoch.zip - Schwerpunktpildung und Berechnung der Regeldifferenz (Eric Hoch, Masterstudent CARE)
 K3_stutz.zip - Schwerpunktpildung und Berechnung der Regeldifferenz (Marc Stutz, Masterstudent Maschinenbau)
K3_stutz.zip - Schwerpunktpildung und Berechnung der Regeldifferenz (Marc Stutz, Masterstudent Maschinenbau)
 K4_Pregler.zip - Herausnahme des Totbereichs beim Motortreiber und einfache P-Regelung der Lenkung.
K4_Pregler.zip - Herausnahme des Totbereichs beim Motortreiber und einfache P-Regelung der Lenkung.
 K5_Pregler_Krit.zip - Regelverstärkung des P-Reglers auf Kkrit eingestellt zur Anwendung des Verfahrens von Ziegler und Nichols (Methode1, s. Kapitel 7 Regelsysteme).
K5_Pregler_Krit.zip - Regelverstärkung des P-Reglers auf Kkrit eingestellt zur Anwendung des Verfahrens von Ziegler und Nichols (Methode1, s. Kapitel 7 Regelsysteme).
 K6_Vortrieb.zip - Erster Versuch die Regelung mit überlagertem Vortrieb zu betreiben. Die Kutsche fährt nun autonom.
K6_Vortrieb.zip - Erster Versuch die Regelung mit überlagertem Vortrieb zu betreiben. Die Kutsche fährt nun autonom.
 K4_PID_Implementiert.zip - vom 26.04.2017
K4_PID_Implementiert.zip - vom 26.04.2017
Ausgangspunkt für weitere Arbeiten:
 K9_OOP.zip - Processing-Programm, Übersichtliche Struktur / Einfügen von 10 Betriebsmodi möglich.
K9_OOP.zip - Processing-Programm, Übersichtliche Struktur / Einfügen von 10 Betriebsmodi möglich.
 K10_OOP.zip - mit P-Regler als modus9.
K10_OOP.zip - mit P-Regler als modus9.
 K11_OOP.zip - neuer Stand P-Regler als extraklasse Regler9.
K11_OOP.zip - neuer Stand P-Regler als extraklasse Regler9.
 MotorAnsteuernSeriell_OOP1.zip - Arduino-Programm, objektorientierte übersichtliche Struktur.
MotorAnsteuernSeriell_OOP1.zip - Arduino-Programm, objektorientierte übersichtliche Struktur.
 K14_Geschw.zip - neuer Stand verbesserte Struktur / Vorlage für PI-Regler / mögliche Geschw.regelung.
K14_Geschw.zip - neuer Stand verbesserte Struktur / Vorlage für PI-Regler / mögliche Geschw.regelung.
Aktueller Stand des Basisprojektes für den Tag der offenen Tür vom 17.5.2017:
 K17_Bildaufzeichnung.zip - verbesserte Programmstruktur insb. iModus
K17_Bildaufzeichnung.zip - verbesserte Programmstruktur insb. iModus
 K18_ALLE_MODI.zip - Version beim Tag der offenen Tür mit Modus 2==Kkrit,4==Sörverhalten,5==adaptiv
K18_ALLE_MODI.zip - Version beim Tag der offenen Tür mit Modus 2==Kkrit,4==Sörverhalten,5==adaptiv
 BILDER.zip - Kamerabilder des Weges bei der ersten "Überlandfahrt" (geschoben!).
BILDER.zip - Kamerabilder des Weges bei der ersten "Überlandfahrt" (geschoben!).
Fortsetzung Vorlesung SoSe 2017
 zustandsregler_mit_beobachter.zip (14.06.2017).
zustandsregler_mit_beobachter.zip (14.06.2017).
 zustandsregler_mit_beobachter_und_sollwert.zip (21.06.2017 Lösung von Herrn Prengel)
zustandsregler_mit_beobachter_und_sollwert.zip (21.06.2017 Lösung von Herrn Prengel)
 zustandsregler_uebung.zip - Musterlösung der Saalübung vom 21.06.2017 mit Scilab.
zustandsregler_uebung.zip - Musterlösung der Saalübung vom 21.06.2017 mit Scilab.
Hinweis: Bei Koordinatentransformation nach ysoll = [xsoll,ysoll] ergibt sich nach Rücktransformation von *-System mit y*=y-ysoll ...
$ \left[\begin{array}{cc}\dot x \\ \dot v\end{array}\right] = Astern \cdot \left[\begin{array}{cc}x \\ v\end{array}\right]-Astern \cdot \left[\begin{array}{cc}xsoll \\ ysoll\end{array}\right] $
Formel 0-1: Ergebnis nach Rücktransformation
Sommersemester 2016
 regelsysteme_20160413.zip - Material von Mittwoch, 13.04.2016, Vorgabe von Polstellen PT2, PD-Regler, I-Anteil im Zeitber., csim.
regelsysteme_20160413.zip - Material von Mittwoch, 13.04.2016, Vorgabe von Polstellen PT2, PD-Regler, I-Anteil im Zeitber., csim.
 regelsysteme_20160419.zip - Material für Dienstag, 19.04, PID Laplace-Transf., Ziegler-Nichols, Korrekte Ableitung des Sollwertes.
regelsysteme_20160419.zip - Material für Dienstag, 19.04, PID Laplace-Transf., Ziegler-Nichols, Korrekte Ableitung des Sollwertes.
 regelsysteme_20160420.zip - Übung.
regelsysteme_20160420.zip - Übung.
 regelsysteme_20160420_lsg.zip - Lösung.
regelsysteme_20160420_lsg.zip - Lösung.
 regelsysteme_20160504.zip - Zwischenstand.
regelsysteme_20160504.zip - Zwischenstand.
 regelsysteme_20160511.zip - Zustandsregler aufgrund identifizierter Regelstrecke auslegen (benötigtes Material)
regelsysteme_20160511.zip - Zustandsregler aufgrund identifizierter Regelstrecke auslegen (benötigtes Material)
 regelsysteme_20160517.zip
regelsysteme_20160517.zip
 regelsysteme_20160607.zip - Nichtlineare Systeme, Phasenraum, Grenzzyklen
regelsysteme_20160607.zip - Nichtlineare Systeme, Phasenraum, Grenzzyklen
 regelsysteme_20160601.zip - Übunge 2 und 3 in Kapitel 13.1
regelsysteme_20160601.zip - Übunge 2 und 3 in Kapitel 13.1
 regelsysteme_20160518.zip - Zustandsregler auf Grundlage der zweiten Identifikation
regelsysteme_20160518.zip - Zustandsregler auf Grundlage der zweiten Identifikation
 regelsysteme_20160525.zip - Aufgabenstellung UND LÖSUNG
regelsysteme_20160525.zip - Aufgabenstellung UND LÖSUNG
 regelsysteme_20160531.zip - Regelbarkeit und Störverhalten
regelsysteme_20160531.zip - Regelbarkeit und Störverhalten
 regelsysteme_20160614.zip - Lösung zum 8.6. und Aufgaben zum 15.6.
regelsysteme_20160614.zip - Lösung zum 8.6. und Aufgaben zum 15.6.
 regelsysteme_20160621.zip - Teillösungen zu 15.6.
regelsysteme_20160621.zip - Teillösungen zu 15.6.
 regelsysteme_20160622.zip - Neufassung
regelsysteme_20160622.zip - Neufassung
 regelsysteme_20160629.zip - Fuzzy-Aufgabe und Scilab-Implementierung
regelsysteme_20160629.zip - Fuzzy-Aufgabe und Scilab-Implementierung
ENDE Sommersemester 2016
Themen Dienstag, 24.03.2015
|
Themen Mittwoch, 25.03.2015
Teil 1
|
Teil 2
|
//Inverse einer Matrix
B=inv(A)
//Transponierte einer Matrix
B=A'
//3x3 Einheitsmatrix
B=eye(3,3);
//Eigenwerte einer Systemmatrix
ew=eye(3,3);
//Beispiel zum Umgang mit Übertragungsfunktionen in Scilab
m = 0.2;
r = 0.03;
D = 0.01;
J = 0.5*m*r*r;
s = poly(0,"s");
G = syslin('c',[1],[J*s*s+D*s]);
R = syslin('c',[5+2*s],[1]);
H = R*G
Q = H/(1+H)
//Pole und Nullstellen der Strecke:
plzr(G)
//Umwandlung in Zustandsform, dann Eigenwerte bestimmen:
strecke=tf2ss(G)
clean(ss2tf(strecke))
Astrecke = strecke(2)//A-Matrix auslesen
ewStrecke = spec(Astrecke)
disp("Eigenwerte der Regelstrecke:")
disp(ewStrecke) //aus einem Skript heraus gezielt anzeigen
//Direkte Simulation der Übertragungsfunktion mit csim:
t = linspace(0,0.001,1000);
anz = size(t);
u = ones(anz(1),anz(2)); //AB bei csim immer Null, Input hier: Sprung auf 1, es folgt daraus die Sprungantwort.
ystrecke = csim(u,t,G);
plot(t,ystrecke(1,:)');
Code 0-1: Scilab-Merkblatt
$ m \ddot y + D \dot y + C y = F $
Formel 0-2: Linearer Schwinger mit Dämpfungselement und äußerer Kraft F.
| m/kg | C/(N/m) | D/(Ns/m) |
|---|---|---|
| 1 | 0 | 2 |
| 2 | 1 | 0 |
| 1 | 1 | 1 |
| 1 | 0 | -1 |
| 1 | 2 | -1 |
Tabelle 0-1: Varianten eines Linearen Schwingers
Einige Übertragungsfunktionen im Zeitbereich als Grundlage für Übungen
$ \ddot x + 3 x = 4 u $
Formel 0-3: a\right)
$ \dot x - x = u $
Formel 0-4: b\right)
$ 3 \ddot x + \dot x = u $
Formel 0-5: c\right)
$ \ddot x + x = u $
Formel 0-6: d\right)
$ \dot x + 2 x = u $
Formel 0-7: e\right)
$ \dot x - 3 x = u $
Formel 0-8: f\right)
$ \dot x + 5 x = 5 u $
Formel 0-9: g\right)
|
Themen Dienstag, 31.03.2015
|
Themen Mittwoch, 01.04.2015
Teil 1
|
|
|
Teil 2
|
|
 simulation_zeit_laplace.zip - Materialien zur Vorlesung am 01.04.2015
simulation_zeit_laplace.zip - Materialien zur Vorlesung am 01.04.2015
 simulation_ziegler.zip - im Unterricht entstanden.
simulation_ziegler.zip - im Unterricht entstanden.
Themen Mittwoch, 08.04.2015
Teil 1
 beispiel_loesung_ziegler_nichols.zip - Beispiel(teil-)lösung zur Anwendung beider Methoden nach Ziegler und Nichols.
beispiel_loesung_ziegler_nichols.zip - Beispiel(teil-)lösung zur Anwendung beider Methoden nach Ziegler und Nichols.
|
|
Teil 2
|
 beispiel_loesung_analyse.zip - Lösung.
beispiel_loesung_analyse.zip - Lösung.
Themen Dienstag, 14.04.2015
|
 pendel_balancieren_optimiert.zip - Optimierung der Regelparameter mittels optim()
pendel_balancieren_optimiert.zip - Optimierung der Regelparameter mittels optim()
Themen Mittwoch, 15.04.2015
Teil 1
|
 pendel_balancieren_optimiert_begrenzt.zip - Musterlösung.
pendel_balancieren_optimiert_begrenzt.zip - Musterlösung.
 pendel_balancieren_eigenwerte.zip - Eigenwertvorgabe und Benutzung von ppol()
pendel_balancieren_eigenwerte.zip - Eigenwertvorgabe und Benutzung von ppol()
Teil 2
|
Themen Dienstag, 21.04.2015
|
 uebung.zip - siehe README.txt in Zip-Verzeichnis.
uebung.zip - siehe README.txt in Zip-Verzeichnis.
Themen Mittwoch, 22.04.2015
Teil 1
|

Bild 0-3: Test des Einachsers
|
|
 musterloesung_aufgabe1_polvorgabe.zip
musterloesung_aufgabe1_polvorgabe.zip
 musterloesung_aufgabe2_polvorgabe.zip
musterloesung_aufgabe2_polvorgabe.zip
Teil 2
Besprechung möglicher Vorgehensweisen zur Regler Herstellung und Reglerauslegung an einem realen System am Beispiel des einachsigen Vehikels:
|
 einachser_programme.zip - Entwicklung eines Mikrocontroller basierten Reglers für ein einachsiges Vehikel
einachser_programme.zip - Entwicklung eines Mikrocontroller basierten Reglers für ein einachsiges Vehikel
HINWEIS: 1. Ersatztermin wg. Abwesenheit ist Donnerstag 23.04.2015, 14-15:30Uhr IWZ135.
Themen Mittwoch, 29.04.2015 (überholt)
 regler_sprung.zip - Material
regler_sprung.zip - Material
Themen Mittwoch, 29.04.2015 (NEU!)
Teil 1 und 2
|
 regler_sprung_kabellos_aufgabe.zip - Aufgaben in README.txt. Besprechung in Vorlesung
regler_sprung_kabellos_aufgabe.zip - Aufgaben in README.txt. Besprechung in Vorlesung
Themen Dienstag, 05.05.2015
Fortsetzung der Aufgabe, optimale Regelparameter für den realen Einachser zu finden
|
clear();
z=300;
u = 0.2*ones(z,1);
t = linspace(0,3,z);
s = poly(0,"s");
pa=0.0246580;
pb=7.9769475;
pc=280.08032;
G = syslin('c',[1],[pa*s*s+pb*s+pc]);
u = 300*ones(z,1);
y = csim(u',t',G);
//plot(t,y(1,:),t,om);
disp("Mit zusätzlichem Integrator um Übertragungsfunktion für Winkel zu bekommen:");
GI = syslin('c',[1],[pa*s*s*s+pb*s*s+pc*s]);
yi = csim(u',t',GI);
//plot(t,yi(1,:),'re',t,phi,'gre',m1(:,1),-m1(:,2)+0.12,'blu');
rp=1200.0;
ri=16.0;
//R=rp+ri/s=(rp*s+ri)/s
R = syslin('c',[rp*s+ri],[s]);
H = R*GI;
Q = H/(1+H);
z=300;
u = 0.2*ones(z,1);
t = linspace(0,3,z);
yq = csim(u',t',Q);
plot(t,yq);
Code 0-2: Zwischenergebnis sprung6c_pi_regler.sce
Themen Mittwoch, 06.05.2015
Teil 1
|
Hinweis: Anfangsbedingungen: [0,0,0,0], Sollwert für phi=0.2rad. Wie kann unmittelbar die Regeldifferenz phisoll-phi aufintegriert werden?
Teil 2
|
clear();
z=300;
u = 0.2*ones(z,1);
t = linspace(0,3,z);
s = poly(0,"s");
pa=0.0246580;
pb=7.9769475;
pc=280.08032;
G = syslin('c',[1],[pa*s*s+pb*s+pc]);
u = 300*ones(z,1);
y = csim(u',t',G);
//plot(t,y(1,:),t,om);
disp("Mit zusätzlichem Integrator um Übertragungsfunktion für Winkel zu bekommen:");
GI = syslin('c',[1],[pa*s*s*s+pb*s*s+pc*s]);
yi = csim(u',t',GI);
//plot(t,yi(1,:),'re',t,phi,'gre',m1(:,1),-m1(:,2)+0.12,'blu');
rp=1200.0;
ri=16.0;
//R=rp+ri/s=(rp*s+ri)/s
R = syslin('c',[rp*s+ri],[s]);
H = R*GI;
Q = H/(1+H);
z=300;
u = 0.2*ones(z,1);
t = linspace(0,3,z);
yq = csim(u',t',Q);
//plot(t,yq);
disp("Darstellung und Simulation von G im Zeitbereich");
Ag=[0,1;-pc/pa,-pb/pa];
Bg=[0;1/pa];
//Vergleichskontrolle der Eigenwerte von G und Ag:
zust=tf2ss(G);
Ag_test=zust(2);
disp(spec(Ag));
disp(spec(Ag_test));
disp("Simulationsmodell für G:");
function f = rechteSeiteG(t,yy)
u_sim = 300.0;
f = Ag*yy+Bg*u_sim;
endfunction
y0 = [0,0]';
t0 = 0;
yg_sim = ode(y0,t0,t,rechteSeiteG);
disp("O.K.: liegen ineinander");
//BEI BEDARF ANZEIGEN LASSEN:
plot(t,yg_sim(1,:),'gre',t,y,'red--');
Code 0-3: Teillösung: G im Zeitbereich.
 teilloesungen.zip - Teillösungen zu obiger Aufgabe.
teilloesungen.zip - Teillösungen zu obiger Aufgabe.
Themen Dienstag, 12.05.2015
|
 regler_sprung_kabellos_loesungen.zip - Lösungen zur Identifikation und Regleroptimierung des Einachsers
regler_sprung_kabellos_loesungen.zip - Lösungen zur Identifikation und Regleroptimierung des Einachsers
Übung 13.1 unten zu Störübertragungsverhalten und Eigenwerte bestimmen und mit Scilab überprüfen.
|
Themen Mittwoch, 13.05.2015
Aktueller Stand zum Einachser und Grundlage für die Herstellung eines Zustandsreglers:

Bild 0-4: SYSTEM0 - Identifiziertes Übertragungsverhalten der Einachser-Strecke zwischen pwm als Eingang und der Winkelgeschwindigkeit ω als Ausgang im Zeitbereich.
a=0.0246580 b=7.9769475 c=280.08032
Code 0-4: Identifizierte Modellparameter.
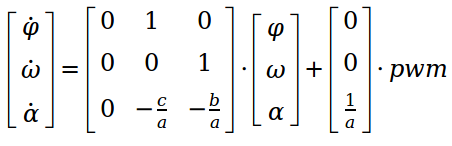
Bild 0-5: SYSTEM1 - Ergänzung des Winkels φ als Zustand. Entspricht dem Hinzufügen eines Integrationsgliedes im Laplace-Bereich.

Bild 0-6: SYSTEM2 - Ergänzung von γ, dem zeitlichen Integral des Winkels φ als Zustand. Entspricht dem weiteren Hinzufügen eines Integrationsgliedes im Laplace-Bereich.
[fopt, xopt, gopt] = optim(list(NDcost,berechneFehler), "b", x0.*0.001, x0.*1000.0, x0); Hinweise zu optim() NDcost - generic external for optim computing gradient using finite differences "b" - If bounds are required, this sequence of arguments must be "b"
Code 0-5: Hinweise zu optim(), Scilab-Hilfe.
Teil 1
Einige Ergänzungen:
|
Teil 1 - Übungen
Lösen Sie die nachfolgenden Aufgaben mit Hilfe von Scilab.
Übung 1
|
 zust_ue1_lsg.zip - Lösungen zur Übung 1.
zust_ue1_lsg.zip - Lösungen zur Übung 1.
Teil 2 - Übungen
Übung 2
|
 zust_ue2_lsg.zip - Lösungen zur Übung 2 (2.1-2.4).
zust_ue2_lsg.zip - Lösungen zur Übung 2 (2.1-2.4).
Themen Dienstag, 19.05.2015
 material_2015_05_18.zip - Beispielortskurve und Bodediagramm
material_2015_05_18.zip - Beispielortskurve und Bodediagramm
|
| Fall | Störgröße | Totzeit | Stellgrößenbegrenzung | P-Anteil | I-Anteil | Skriptname |
|---|---|---|---|---|---|---|
| 1 | nein | nein | nein | 22408.928 | 0.016 | sprung8... |
| 2 | nein | nein | ja | 7432.5858 | 0.016 | sprung9... |
| 3 | nein | ja | ja | 3736.0204 | 0.016 | sprung12... |
| 4 | st=0.01 | ja | ja | 3237.6 | 191.88704 | sprung12c... |
| 5 | st=0.03 | ja | ja | 1956.4263 | 166.4572 | sprung12c... |
Tabelle 0-2: Regler-Optimierungsergebnisse für die angenäherte Übertragungsfunktion des Einachsers.

Bild 0-7: Simulationsergebnisse mit Dummy-Parametern (grün), optimiert Fall 1 (rot), optimiert Fall 4 (blau).
 einachser026_simtest.zip - Test der optimierten Parameter am realen System.
einachser026_simtest.zip - Test der optimierten Parameter am realen System.
Themen Mittwoch, 20.05.2015
Teil 1 und 2
Fortsetzen der Themen von Dienstag und...
|
 einachser025.zip - Vergleichsreferenz (Werden Sie besser als dieser Regler)
einachser025.zip - Vergleichsreferenz (Werden Sie besser als dieser Regler)
Themen Dienstag, 02.06.2015
|
Themen Mittwoch, 03.06.2015
Teil 1
|
Teil 2
|
Themen Dienstag, 09.06.2015
|
Themen Mittwoch, 10.06.2015
Teil 1
|
Teil 2
|
Einführung
Regelkreise werden in technischen Systemen beispielsweise verwendet, um:
|
An diesen Beispielen wird deutlich, dass es Regelungssysteme gibt, die auf ganz unterschiedlichen physikalischen Größen agieren. Geregelt werden beispielsweise Druck, Temperatur, Ort, Geschwindigkeit, Winkel, Winkelgeschwindigkeit, Kraft, Moment, Strom, Spannung, Leistung usw.
Alle diese erwähnten Systeme weisen aber eine ähnliche Struktur auf.
|
Aus dem Wunsch heraus aus dieser Gemeinsamkeit eine übergreifende Wissenschaft ins Leben zu rufen, geht die Begründung der Kybernetik durch Norbert Wiener in den 1970er Jahren hervor.
Es soll nicht verschwiegen werden, dass diese Wissenschaft auf technischen Entwicklungen fußt, die im Zweiten Weltkrieg gemacht wurden. Insbesondere wurden in England unter Verwendung des Radars automatische Nachführungen für Flug-Abwehr-Geschütze entwickelt.
War der Begriff des Regelkreises erst einmal klar gefaßt, wurden diese auch in Nicht-technischen Systemen identifiziert:
|
Regelsysteme, die in der Lage sein sollen Störungen zu kompensieren und nicht zu verstärken,
Um den prinzipiellen Aufbau eines Regelungstechnischen Systems zu verdeutlichen, wird im folgenden Unterkapitel ein einfaches Regelungssystem vorgestellt, anhand dessen die allgemein gültige Grundstruktur aufgezeigt wird.