|
Der Windup-Effekt bei Reglern mit begrenzten Stellgrößen
 windup.zip - Download der im folgenden entwickelten C++ - Programme.
windup.zip - Download der im folgenden entwickelten C++ - Programme.
- Schon mehrfach innerhalb dieser Vorlesung tauchten zwei Fragestellungen auf:
- Wie kann man in einem Regelkreis mit Stellgrößen-Gebern mit begrenztem Wertebereich umgehen? - Beispiel Geschwindigkeitsregelung: Es war nur ein PWM-Signal zwischen -1023 und +1023 möglich.
- Kann es passieren, dass der I-Anteil eines PID-Reglers durch auftretende Störungen so weit wächst, dass der Regelkreis, in dem er eingebaut ist, instabil wird?
- Um einer Verwirrung bei den nachfolgenden Versuchen vorzubeugen, soll schon vorab beschrieben werden, was der Windup-Effekt ist.
|
Was ist der Windup-Effekt?
- Die Stellgröße eines Regelkreises sei begrenzt und der Regler besitze einen I-Anteil.
- Wird ein Sollwert angestrebt, bei dem die Stellgröße in die Sättigung geht, so kann die Strecke über einen langen Zeitraum nicht ausgeregelt werden.
- Als Nebeneffekt wird der I-Anteil ständig erhöht (windup).
- Tritt dann später als Sollwert ein Wert auf, der eigentlich gut ausgeregelt werden kann und bei dem die Stellgröße nicht in die Sättigung gehen müßte, so kann es zu einem starken Überschwingen oder sogar zur Instabilität des Reglers führen, da der hohe I-Anteil zunächst durch Überschwingen wieder abgebaut wird.
|
Besteht bei der Geschwindigkeitsregelung des COACH-Vehikels die Gefahr eines Windup-Effektes?
- Schauen wir uns hierzu zunächst die C++-Simulation dieses Regelkreises mit optimierten Parametern an.
- Das zugehörige Simulationsmodell kann folgendermaßen realisiert werden:
|
class ModellRegelkreis
{
private:
double w,e,de,ie,u;
int anzahl;
public:
double K,T,d,P,I,D,pwm,i_anteil;
ModellRegelkreis()
{
anzahl = 3;
K=30.552649;
T=0.0255439;
d=2.0995919;
//Optimierte Parameter (Stellgröße bleibt in erlaubten Grenzen):
P=51.1;
I=335.35;
D=0.768;
//Parameter, um einen schnelleren Regler zu realisieren.
//Die Stellgröße erreicht hier unerlaubte Werte.
/*
P=100.0;
I=1000.0;
D=0.768;
*/
pwm=0.0;
i_anteil = 0.0;
}
int holeAnzahlGleichungen()
{
return anzahl;
}
double rechteSeite(double* y,double t, int zeile)
{
w = 20.0; //Sollwert in Omega_vierteln-Einheiten
if(t>0.25)
w=5.0;
e = w-y[0]; //Regeldifferenz
de = -y[1]; //Für konstantes w ist dies die Ableitung der Regeldifferenz
ie = y[2]; //Integral der Regelabweichung
pwm = P*e + I*ie + D*de;
i_anteil = I*ie;
u=pwm/1023.0;
switch(zeile)
{
case 0:
return y[1];
break;
case 1:
return -(1.0/(T*T))*y[0]-(2.0*d/T)*y[1]+(K/(T*T))*u;
break;
default:
return e;
break;
}
}
};
Code 0-1: ModellRegelkreis.h aus dem C++ Projekt cpp1_regelkreis_windup03a - Simulationsmodell für Geschwindigkeitsregelung
- Von einem Sollwert bei w=20 wird nach 0,25 Sekunden auf einen von w=5 umgeschaltet.
- Der nachfolgende Plot des Stellsignals (PWM) zeigt, dass der Regler Stellsignale innerhalb des erlaubten Bereiches (-1023..+1023) liefert.
- Die Parameter des Regelkreises wurden auch so optimiert, dass die Stellgröße in dem erlaubten Bereich bleibt.
- Leider ist die Regelung so langsam, dass die Sollwerte innerhalb der simulierten Zeit gar nicht voll erreicht werden (Kriechverhalten).
- Ergänzend wird auch die Entwicklung des I-Anteils mit ausgegeben.
|

Bild 0-1: Verlauf von Winkelgeschwindigkeit, PWM-Signal und I-Anteil bei Verwendung optimierter Regelparameter.
- Um den Regler schneller zu machen, werden willkürlich der P-Anteil und der I-Anteil erhöht:
- P=100
- I=1000
- D=0.768 (unverändert)
|

Bild 0-2: Verlauf von Winkelgeschwindigkeit, PWM-Signal und I-Anteil bei Verwendung von Parametern, die zu überhöhten Stellsignalen führen.
- Nun werden die Sollwerte schnell erreicht.
- Allerdings treten Stellsignale auf, die zeitweise um den Faktor 10 größer als die möglichen/erlaubten sind.
- Der I-Anteil nimmt hier so wie bei der ersten Simulation keine überhöhten Werte an.
|
- Als nächstes soll die Stellgröße unter Beibehaltung des letzten Parametersatzes auf den erlaubten Bereich beschränkt werden.
- Das heißt, bevor das durch den Regler erzeugte Stellsignal auf die Strecke gegeben wird, wird auf dieses noch eine Sättigungsfunktion angewendet.
- Die Sättigungsfunktion läßt sich folgendermaßen mathematisch formulieren:
|

Bild 0-3: Sättigungsfunktion für das PWM-Signal.
- Als Blockschaltbild läßt sich die neue Situation folgendermaßen darstellen:
|

Bild 0-4: Blockschaltbild zu einem Regelkreis mit Sättigungsglied.
- Im Modell läßt sich das Sättigungsglied sehr leicht durch zwei Verzweigungsbedingungen realisieren:
|
...
double rechteSeite(double* y,double t, int zeile)
{
w = 20.0; //Sollwert in Omega_vierteln-Einheiten
if(t>0.25)
w=5.0;
e = w-y[0]; //Regeldifferenz
de = -y[1]; //Für konstantes w ist dies die Ableitung der Regeldifferenz
ie = y[2]; //Integral der Regelabweichung
pwm = P*e + I*ie + D*de;
i_anteil = I*ie;
//Beginn des Sättigungsgliedes
if(pwm>1023.0)
pwm = 1023.0;
if(pwm<-1023.0)
pwm = -1023.0;
//Ende des Sättigungsgliedes
u=pwm/1023.0;
switch(zeile)
{
case 0:
return y[1];
break;
case 1:
return -(1.0/(T*T))*y[0]-(2.0*d/T)*y[1]+(K/(T*T))*u;
break;
default:
return e;
break;
}
}
...
Code 0-2: rechteSeite(..) in ModellRegelkreis.h aus dem C++ - Projekt cpp1_regelkreis_windup03a mit eingefügter Sättigungsfunktion.
- Im folgenden sind auch hierzu die Schaubilder zusehen:
|

Bild 0-5: Verlauf von Winkelgeschwindigkeit, PWM-Signal und I-Anteil bei Verwendung von Parametern, die zu überhöhten Stellsignalen führen, jedoch mit nachgeschaltetem Sättigungsglied.
- Den Schaubildern ist zu entnehmen, dass der nun entstandene Regelkreis keinen, zumindest keinen störenden, Windup-Effekt aufweist.
- Im Gegenteil: Die Regeleigenschaften mit dem nun eingefügten Sättigungsglied sind besser als die bei den "optimierten" Parametern:
- Die Sollwerte werden hier schneller erreicht, als bei der ersten Simulation.
- Der I-Anteil wird schnell genug abgebaut, um auch den zweiten Sollwert schnell erreichen zu können.
|
- Gerade wenn aber mit Integerwerten bei der Realisierung des Reglers auf einem Mirkocontroller gearbeitet wird, sollte aber der auftretende Wertebereich des I-Anteils kontrolliert werden, bzw. künstlich begrenzt werden, um keine Überläufe zu produzieren und damit völlig unkontrollierte Vorzeichenwechsel.
|
Wie läßt sich ein Windup-Effekt provozieren?
- Nachdem nun die Einführung eines Sättigungsgliedes eundeutig zur Verbesserung des Regelkreises geführt hat, stellt sich nun die Frage, unter welchen Bedingungen ein sich schädlich auf die Regeleigenschaften auswirkender Windup-Effekt auftritt.
|
- Ist ein Sollwert nicht erreichbar, so sollte der I-Anteil besonders stark wachsen.
- Der erste Sollwert wird testweise auf 100 gesetzt:
|
double rechteSeite(double* y,double t, int zeile)
{
// w = 20.0; //Sollwert in Omega_vierteln-Einheiten
//Vorgabe eines nicht erreichbaren Sollwertes:
w = 100.0;
if(t>0.25)
w=5.0;
...
Code 0-3: Ausschnitt aus rechteSeite(..) in ModellRegelkreis.h aus dem C++ - Projekt cpp1_regelkreis_windup03a mit nicht erreichbarem Sollwert.

Bild 0-6: Verlauf von Winkelgeschwindigkeit, PWM-Signal und I-Anteil, gleicher Parametersatz wie zuvor mit Sättigungsfunktion unter Verwendung eines nicht erreichbaren Sollwertes.
- Hier stellt sich nun eine Situation ein, die eindeutig als Windup-Effekt zu erkennen ist:
- Da der vorgegebene Sollwert mit Hilfe des verfügbaren Stellgrößenbereiches von -1023 bis +1023 nicht erreichbar ist, steigt der I-Anteil zu Beginn der Simulation extrem an.
- Nach dem Wechsel des Sollwertes nach 0,25 Sekunden kann der I-Anteil im Verlauf der restlichen Simulation nicht einmal soweit abgebaut werden, dass sich irgendetwas an dem Stellsignal ändert.
- Es belibt die ganze Zeit auf +1023 stehen.
|
Erstes Fazit
- Solange also der Sollwert in einem realisierbaren Bereich bleibt, läßt sich sogar mittels extremer Regelparameter und eines Sättigungsgliedes ein verbessertes Regelverhalten gegenüber einem reinen PID-Regler erreichen.
- Treten jedoch auch überhöhte Sollwerte auf, so wird der Regler durch die Aufsummation des I-Anteils schnell unbrauchbar.
|
Läßt sich der Windup-Effekt vermeiden?
Einführung von Antiwindup-Elementen
- Ein gängiges Antiwindup-Element besteht in einer Vorrichtung, die die Überhöhung der Stellgröße über das erlaubte Maß negativ auf den I-Anteil rückkoppelt.
- Befindet sich die Stellgröße also im erlaubten Bereich passiert nichts. Hier hat das Antiwindup-Element eine Totzone.
- Übersteigt sie aber den erlaubten Grenzwert, so der Überhöhungsanteil mit einem Proportionalitätsfaktor von dem I-Anteil abgezogen.
- Eine negative Integralbildung wird der über die Regelabweichung hinzugefügt.
|
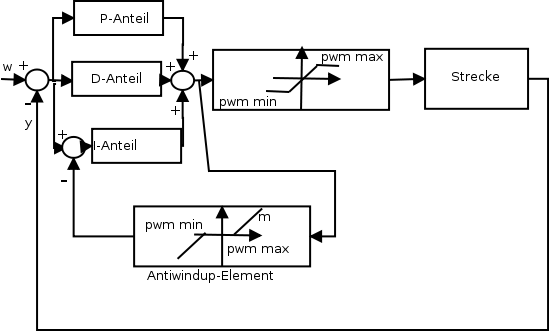
Bild 0-7: Blockschaltbild des Regelkreises mit PID-Regler, Sättigungselement und Antiwindup-Element.
- Für die Steigung m des Antiwindup-Elements ist zu berücksichtigen, dass die Regelabweichung, gegen die das Antwindup angeht ca. um Faktor 50 kleiner ist.
- Es ergibt sich bei der Simulation folgendes Bild:
|

Bild 0-8: Verlauf von Winkelgeschwindigkeit, PWM-Signal und I-Anteil, gleicher Parametersatz wie zuvor mit Sättigungsfunktion unter Verwendung eines nicht erreichbaren Sollwertes und zusätzlich eines Antiwindup-Elements.
- Nun reagiert der Regelkreis wieder auf die Sollwertänderung, da der I-Anteil schnell früh abgebaut wird.
- Bei einer Implementierung ist hier aber zu beachten, dass zeitweise auch sehr große I-Anteile entstehen.
- Das Antiwindup-Element wurde folgendermaßen implementiert:
|
class ModellRegelkreis
{
private:
double w,e,de,ie,u;
int anzahl;
public:
double K,T,d,P,I,D,pwm,i_anteil;
double anti,m;
ModellRegelkreis()
{
anzahl = 3;
//Proportionalitätsfaktor für Antiwindup-Element:
m=0.05;
K=30.552649;
T=0.0255439;
d=2.0995919;
//Parameter, um einen schnelleren Regler zu realisieren.
//Die Stellgröße erreicht hier unerlaubte Werte.
P=500.0;
I=1000.0;
D=0.768;
pwm=0.0;
i_anteil = 0.0;
}
int holeAnzahlGleichungen()
{
return anzahl;
}
double rechteSeite(double* y,double t, int zeile)
{
// w = 20.0; //Sollwert in Omega_vierteln-Einheiten
//Vorgabe eines nicht erreichbaren Sollwertes:
w = 100.0;
if(t>0.25)
w=5.0;
e = w-y[0]; //Regeldifferenz
de = -y[1]; //Für konstantes w ist dies die Ableitung der Regeldifferenz
ie = y[2]; //Integral der Regelabweichung, von der aber nun auch das Antiwindup-Element abgezogen wird.
pwm = P*e + I*ie + D*de;
i_anteil = I*ie;
//Aktueller Wert für das Antiwindup-Element:
anti = 0.0;
if(pwm>1023.0)
anti = m*(pwm-1023);
if(pwm<-1023.0)
anti = m*(pwm+1023);
//Beginn des Sättigungsgliedes
if(pwm>1023.0)
pwm = 1023.0;
if(pwm<-1023.0)
pwm = -1023.0;
//Ende des Sättigungsgliedes
u=pwm/1023.0;
switch(zeile)
{
case 0:
return y[1];
break;
case 1:
return -(1.0/(T*T))*y[0]-(2.0*d/T)*y[1]+(K/(T*T))*u;
break;
default:
return e-anti; //Aktuellen Antiwindup-Anteil abziehen.
break;
}
}
};
Code 0-4: Modell mit Antiwindup-Element in Projekt cpp1_regelkreis_antiwindup03a.
- Bleiben nun mit dem Antiwindup-Element die positiven Eigenschaften des Reglers für passende Sollwertvorgaben erhalten?
- Folgende Schaubilder wurden aus der Simulation von obigem Modell mit w=20 gewonnen:
|

Bild 0-9: Verlauf von Winkelgeschwindigkeit, PWM-Signal und I-Anteil, gleicher Parametersatz wie zuvor mit Sättigungsfunktion unter Verwendung eines erreichbaren Sollwertes und zusätzlich eines Antiwindup-Elements.
- Die Schaubilder zeigen, dass die Regeleigenschaften für sinnvolle Sollwerte mit dem Antiwindup-Element nun nicht mehr so gut sind, wie ohne.
- Die naheliegende Lösung wäre, auf das Antiwindup-Element zu verzichten und für Sollwerte in einem umsetzbaren Bereich zu sorgen.
|
Aufgabe
- Suchen Sie nach einem besseren Parameter m für das Antiwindup-Element.
- Versuchen Sie dann die gleichen Modell- und Regelungserweiterungen wie weiter oben für die Antriebsregelung für diese Strecke durchzuführen.
- Das .zip-File am Anfang des Kapitels enthält auch eine PC-Simulation für die Lenkung.
- Sind die Ergebnisse ähnlich? Oder ergeben sich durch den I-Anteil der Strecke bei der Lenkung andere Situationen?
|
|
 windup.zip - Download der im folgenden entwickelten C++ - Programme.
windup.zip - Download der im folgenden entwickelten C++ - Programme.








