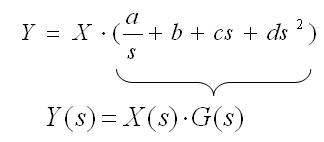Einführung in die Anwendung der Laplace-Transformation
- In der Regelungstechnik verwendet man Übertragungsglieder zur Darstellung der Komponenten eines Regel-Systems.
- Diese lassen sich aus den gegebenen Gleichungen / Differentialgleichungen durch eine Transformationsvorschrift gewinnen.
- Der Vorteil beim Umgang mit diesen Transformierten sind die sehr einfachen Rechenregeln für deren Reihen- und Parallelschaltung.
- Die Transformationsvorschrift für eine Funktion im Zeitbereich f(t) lautet:
|

Bild 0-1: Laplace-Transformation
- Es handelt sich hier um ein so genanntes Faltungsintegral.
- Eine Gewichtsfunktion wird mit f multipliziert und über jeden Zeitpunkt aufintegriert.
- Ohne das δ in s handelte es sich bei der Zusatzfunktion um
eine Kreisschwingung mit variabler Frequenz.
- Nähme man ein konkretes ω1 heraus, würde man f zu jedem
Zeitpunkt mit dieser konkreten Schwingung gewichten.
- D.h. je eher f der Schwingung entspricht, desto
größer fällt ihr Faltungsintegral an der Stelle ω1 aus.
- Man erhält also eine Funktion F(s), die aussagt, wie gut
f(t) die Funktion e-ts an einer beliebingen Stelle
s abbildet.
- Das besondere an der Sache ist, dass es auch eine eindeutige
Vorschrift gibt, wie man aus F(s) wieder f(t) gewinnt:
|

Bild 0-2: Laplace-Rück-Transformation
- Mit Hilfe bekannter elementarer Laplace-Transformationen
können die Laplace-Transformierten zusammengesetzter Funktionen ermittelt werden.
- Insbesondere ergibt die n-te Differentation im Zeitbereich als
Transformierte eine bloße Multiplikation sn.
- Eine Integration im Zeitbereich bedeutet die Division durch s
im Bildbereich.
- Eine Multiplikation mit einer Konstanten bleibt erhalten.
- Hier ein elementares Beispiel (a,b,c,d: konstante Faktoren):
|

Bild 0-3: Laplace-Transformation einer Differential/Integtralgleichung
- x,y der Gleichung im Zeitbereich sind Funktionen der Zeit: x(t), y(t)
- X,Y der Gleichung im Bildbereich sind Funktionen von s: X(s), Y(s)
- Durch die Möglichkeit X(s) vorzuziehen, wird es möglich,
die Funktion in der X drin stand für sich als "Übertragungsfunktion" G(s) zu betrachten:
|
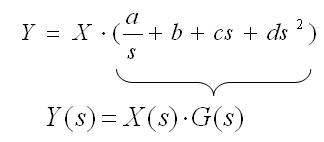
Bild 0-4: Eingangsgröße X, Ausgangsgröße Y und Übertragungsfunktion G im Bildbereich