Entwurf eines Zustandsreglers mit Beobachter
(EN google-translate)
(PL google-translate)
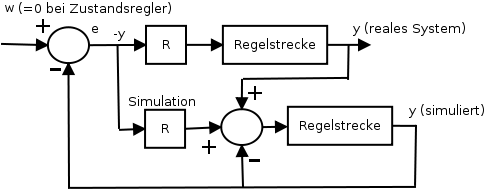
Bild 0-1: Prinzip des Zustandsreglers mit Beobachter und Angleichung zwischen Simulation und realem System durch Rückführung der Differenz von yreal - ysim auf den Eingang der simulierten Strecke.
Um eine realistische Umsetzung zu erhalten, wird der Zustandsregler von einem numerisch rekonstruierten Zustand gespeist und mit einem einfachen Integrationsverfahren parallel zum realen Modell simuliert.
Als Besonderheit wird zunächst das Euler-Verfahren und dann das implizite Eulerverfahren verwendet und miteinander verglichen.
Integration mit Euler vorwärts
 007_beobachter.zip - Skripte zur realisierung des Zustandsreglers mit Beobachter des Einachsers als Simulation mit Euler vorwärts.
007_beobachter.zip - Skripte zur realisierung des Zustandsreglers mit Beobachter des Einachsers als Simulation mit Euler vorwärts.
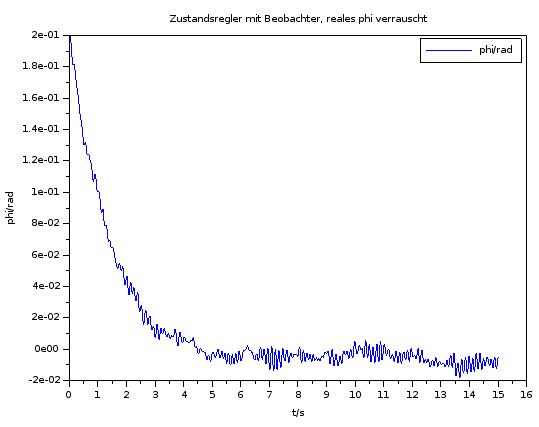
Bild 0-2: Simulationsergebnis zum Zustandsregler mit Beobachter. Integration mit Euler vorwärts. FEHLERHAFTES Skript: u_begrenzt_aktuell = -RR*ynum + LL*(ynum-ysim);
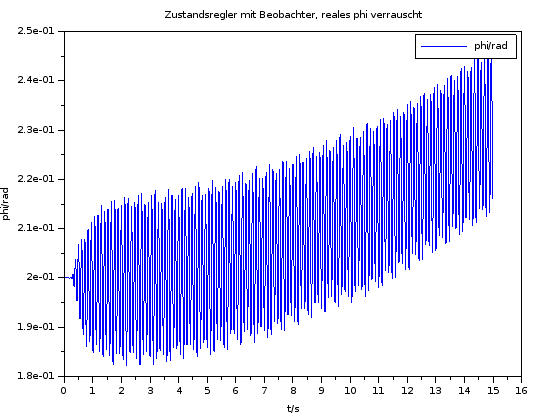
Bild 0-3: Simulationsergebnis zum Zustandsregler mit Beobachter. Integration mit Euler vorwärts. KORRIGIERTES Skript: u_begrenzt_aktuell = -RR*ysim + LL*(ynum-ysim);
function ygir_sim=simulation(x,y0,t)
RR = [x(1),x(2),x(3),x(4)];
zs=size(t);
z=zs(2);
t0 = 0;
yalt = y0;
ygir_sim = yalt
u_begrenzt_aktuell = 0;
u_merk = [0];
index_umerk = 1;
//Für die numerische Bestimmung der Zustandsgrößen
phi = y0(1);
phi_alt = y0(1);
phi_integ = 0.0;
omega = 0.0;
omega_alt = 0.0;
s_int=0.0;
s_phi=0.0;
s_ome=0.0;
s_alf=0.0;
for i=1:1:z-1
takt = t(i);
phi_alt = phi;
omega_alt = omega;
phi = yalt(1) + grand(1, 1, "nor", MITTELWERT, STREUUNG);
// phi = yalt(1);
phi_integ = phi_integ + phi*dt;
omega = (phi - phi_alt)/dt;
alfa = (omega - omega_alt)/dt;
//Numerisch rekonstruierter Zustand:
ynum = [phi_integ;phi;omega;alfa];
//weiteren Zustand durch Simulation rekonstruieren:
s_int = s_int + s_phi*dt;
s_phi = s_phi + s_ome*dt;
s_ome = s_ome + s_alf*dt;
s_alf = s_alf + ( (-pc/pa)*s_ome + (-pb/pa)*s_alf + (1/pa)*u_begrenzt_aktuell )*dt;
ysim = [s_int;s_phi;s_ome;s_alf];
//Korrekturfaktor, um simuliertes y nahe an das reale zu holen:
LL = [1.0,100.0,1.0,0.1]; //phi am stärksten gewichten
//Zeitschritt durchführen:
yneu=ruku(yalt,takt,dt);
ygir_sim=[ygir_sim,yneu];
yalt=yneu;
//Erst danach das Stellsignal aktualisieren:
//u_begrenzt_aktuell = -RR*ynum + LL*(ynum-ysim); FEHLERHAFT
u_begrenzt_aktuell = -RR*ysim + LL*(ynum-ysim); //RICHTIG, liefert aber keine vernünftigen Erg., jedoch Euler implizit. s.u.
if u_begrenzt_aktuell>480 then
u_begrenzt_aktuell=480;
end
if u_begrenzt_aktuell<-480 then
u_begrenzt_aktuell=-480;
end
end
endfunction
Code 0-1: simulation.sce - Das mit-integrierte Beobachtermodell wird hier so realisiert, wie das auch innerhalb eines Mikrocontrollerprogramms geschehen würde: Der reale Systemzustand wird numerisch rekonstruiert, die Modellintegration erfolgt sehr einfach mittels Euler-Integration.
Integration mit implizitem Euler-Verfahren
 008_beobachter_impl_euler.zip - Scilab-Skripte zu nachfolgender Darstellung.
008_beobachter_impl_euler.zip - Scilab-Skripte zu nachfolgender Darstellung.
$ \vec y_\left(k+1\right) = \left(E-A \cdot \Delta t\right)^\left(-1\right) \cdot \left( \vec y_k+B \cdot \vec u_k \cdot \Delta t\right) $
Formel 0-1: Implizites Eulerverfahren bei bekannter Systemmatrix \left(vergl. Herleitung in übergeordnetem Kapitel\right).
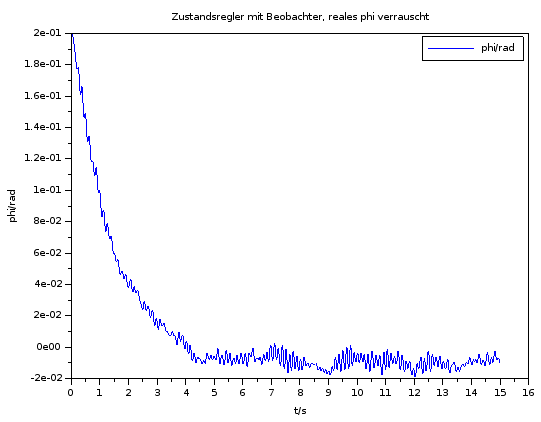
Bild 0-4: Simulationsergebnis bei Verwendung des impliziten Eulerverfahrens statt des expliziten.
Nach Korrektur des Skripts für Euler Vorwärts ist nun deutlich die Verbesserung mit dem impliziten Eulerverfahren zu sehen: Beim Euler-Vorwärts regelt das System bei dieser Schrittweite gar nicht aus.
function ygir_sim=simulation(x,y0,t)
RR = [x(1),x(2),x(3),x(4)];
zs=size(t);
z=zs(2);
t0 = 0;
yalt = y0;
ygir_sim = yalt
u_begrenzt_aktuell = 0;
u_merk = [0];
index_umerk = 1;
//Für die numerische Bestimmung der Zustandsgrößen
phi = y0(1);
phi_alt = y0(1);
phi_integ = 0.0;
omega = 0.0;
omega_alt = 0.0;
s_int=0.0;
s_phi=0.0;
s_ome=0.0;
s_alf=0.0;
//Vorbereitung für das implizite Eulerverfahren:
// yk+1 = inv(E-A*dt)*(yk+B*uk*dt)
// yk+1 = AI*(yk+B*uk*dt)
AI = inv(eye(4,4)-Agii*dt);
ysim = [0;0;0;0];
for i=1:1:z-1
takt = t(i);
phi_alt = phi;
omega_alt = omega;
phi = yalt(1) + grand(1, 1, "nor", MITTELWERT, STREUUNG);
// phi = yalt(1);
phi_integ = phi_integ + phi*dt;
omega = (phi - phi_alt)/dt;
alfa = (omega - omega_alt)/dt;
//Numerisch rekonstruierter Zustand:
ynum = [phi_integ;phi;omega;alfa];
//weiteren Zustand durch Simulation rekonstruieren:
ymodell = ysim;
//implizites Euler-Verfahren:
ysim = AI*(ymodell+Bgii*u_begrenzt_aktuell*dt);
//Korrekturfaktor, um simuliertes y nahe an das reale zu holen:
LL = [1.0,100.0,1.0,0.1]; //phi am stärksten gewichten
//Zeitschritt durchführen:
yneu=ruku(yalt,takt,dt);
ygir_sim=[ygir_sim,yneu];
yalt=yneu;
//Erst danach das Stellsignal aktualisieren:
u_begrenzt_aktuell = -RR*ynum + LL*(ynum-ysim);
if u_begrenzt_aktuell>480 then
u_begrenzt_aktuell=480;
end
if u_begrenzt_aktuell<-480 then
u_begrenzt_aktuell=-480;
end
end
endfunction
Code 0-2: simulation.sce - Das mit-integrierte Beobachtermodell wird hier so realisiert, wie das auch innerhalb eines Mikrocontrollerprogramms geschehen würde: Der reale Systemzustand wird numerisch rekonstruiert, die Modellintegration erfolgt mittels impliziter Euler-Integration.