Umsetzung einfacher Regelkreise mit Scilab
- Der folgende Quellcode repräsentiert den P-Regelkreis des vorangegangenen Kapitels.
|
function f = rechteSeite(t,y)
u=0.7-y(1,1);
f(1,1)=y(2,1);
f(2,1)=-y(1,1)-2.0*y(2,1)+u;
endfunction
t = 0:0.01:30;
y0 = [0,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)');
Code 0-1: P-Regler für Heizregelung
Übung 3
- Durch Hinzufügen eines differentiellen Anteils zu dem Regler, kann erreicht werden, dass der Sollwert schneller erreicht wird.
- Fügen Sie testweise in das vorangegangene Beispiel einen D-Anteil hinzu, indem Sie auch noch y(1,2) von u abziehen.
- Inwiefern verändert dies das Reglerverhalten?
- Wie sieht das passende Blockschaltbild hierzu aus?
- Realisieren Sie das gleiche System in Scicos.
- Erst wenn die Regelabweichung aufintegriert wird und das Ergebnis ebenfalls zurückgeführt wird, kann vermieden werden, dass es eine bleibende Regelabweichung gibt.
- Wie kann in dem Scilab-Programm und dem korrespondierenden Scicos-Programm dem Regler ein Integralanteil hinzugefügt werden?
- Hinweise zum PID-Regler:
|
Der PID-Regler
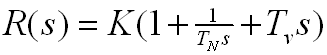
Bild 0-5: PID-Regler allgemein
- K: proportionaler Verstärkungsfaktor
- TN: Nachstellzeit: Benötigte Zeit, um eine Sprungantwort auszugleichen.
- Ohne I-Anteil bleibt stets eine bleibende Regelabweichung erhalten.
- Der I-Anteil führt zu einer Phasendrehung, die zu einem Aufschwingen führen kann.
- Deshalb kann kein zu großer K-Wert mit I-Wert zusammen eingestellt werden.
- Dann allerdings reagiert der Regler träge.
- Das ist auch genau der Nachteil des PI-Reglers.
- Abhilfe schafft die Einführung eines D-Anteils.
- Der D-Anteil reagiert schon auf Änderungen der Regeldifferenz.
- D-Glieder "erkennen Trends", reagieren aber empfindlich auf verrauschte Eingangssignale.
|
Übung 3b
- In Kapitel 5.2 wird der Regler mit Hilfe der Funktion optim in Scilab optimiert. Testen und analysieren Sie das Beispiel als Vorbereitung auf die nächste Vorlesung.
|