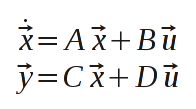Standarddarstellung linearer Übertragungsglieder im Zeitbereich
(EN google-translate)
(PL google-translate)

Bild 0-1: Prinzip-Blockschaltbild eines Zustandsreglers.
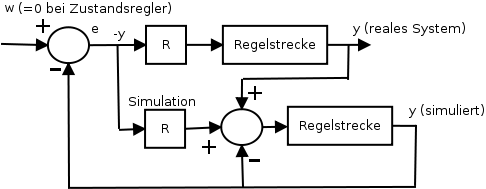
Bild 0-2: Zustandsregler mit Beobachtermodell: Die Differenz zwischen realem Systemzustand und simuliertem Systemzustand wird auf den Eingang der simulierten Regelstrecke rückgekoppelt.
Ergänzung: Standarddarstellung linearer Übertragungsglieder im Zeitbereich
- Die folgende Darstellung ist die Standarddarstellung linearer Übertragungsglieder im Zeitbereich.
- Die Bedeutung der einzelnen Matrizen ist die folgende:
- A: Systemmatrix
- B: Eingangsmatrix
- C: Ausgangsmatrix
- D: Durchgangsmatrix
|
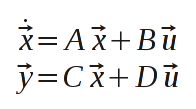
Bild 0-4: Standarddarstellung linearer Übertragungsglieder im Zeitbereich als DGLS erster Ordnung.
- Häufig ist bei den hier betrachteten Systemen die Ausgangsmatrix C die Einheitsmatrix und die Durchgangsmatrix die Nullmatrix.
|
- x: Zustandsvektor n x 1
- u: Eingangsvektor r x 1
- y: Ausgangsvektor m x 1
|
- A: Systemmatrix n x n
- B: Eingangsmatrix n x r
- C: Ausgangsmatrix m x n
- D: Durchgangsmatrix m x r
|
Zustandsregler mit Beobachter
- Beim Einsatz von Zustandseglern bei realen Regelstrecken tritt häufig das Problem auf, dass sich nicht alle der zurückzuführenden Zustandsgrößen auch an der Regelstrecke messen lassen.
- Eine Lösung für dieses Problem stellt dar, parallel zur Regelung eine Simulation der geregelten Strecke mitlaufen zu lassen und von dort die fehlenden Zustandsgrößen abzugreifen.
- Im (natürlich unrealistischen) Idealfall könnte man auch sämtliche Zustandsgrößen simulieren und diese auf die Simulation und das reale System multipliziert mit der Regelmatrix R negativ zurückführen:
|

Bild 0-5: Idealfall Zustandsregler mit Beobachter-Modell: der simulierte Zustandsvektor wird auf das reale System und das simulierte zurückgeführt.
- Ein solches Konzept kann aus folgenden Gründen nicht funktionieren:
|
- Das Modell bildet nicht exakt das reale System ab. Beide Zustandsverläufe driften nach einiger Zeit auseinander.
- Beim realen System treten Störungen auf, die im Modell nicht mit abgebildet werden, weshalb der Regler falsch reagieren würde.
- Die Anfangsbedingungen des realen Systems sind i.d.R. nicht genau genug bekannt. Die Simulation würde deshalb an einem vom realen System abweichenden Zustand starten.
|
- Das Konzept wird aber praktisch anwendbar, wenn die Differenz zwischen realem und simuliertem Zustand y zusätzlich auf den Eingang der Simulation zurückgeführt wird.
- Das entsprechende Schaubild sieht dann folgendermaßen aus:
|

Bild 0-6: Zustandsregler mit Beobachtermodell: Die Differenz zwischen realem Systemzustand und simuliertem Systemzustand wird auf den Eingang der simulierten Regelstrecke rückgekoppelt.
- Um die Wirksamkeit der Rückkopplung der Differenz zwischen realer und simulierter Zustandsgröße einstellen zu können, wird noch eine Gewichtsmatrix L eingeführt.
- Sinnvollerweise werden nur diejenigen Zustände aus der Simulation verwendet, die sich nicht direkt messen lassen.
|