Day by Day
(EN google-translate)
(PL google-translate)
Verzeichnis der im Verlauf des Semesters behandelten Themen
 siehe auch day_by_day vom Wintersemester 2020/21: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21
siehe auch day_by_day vom Wintersemester 2020/21: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21
Dienstag 16.03.2021
|
Einführung in Regelungstechnik
 62_Regelungssysteme/02_Heizregelkreis
62_Regelungssysteme/02_Heizregelkreis
Einführung in Scilab
 37_Scilab
37_Scilab
 50_Simulationstechnik/01_Systemtheorie/07_scilab
50_Simulationstechnik/01_Systemtheorie/07_scilab
Übung 1
|
$ \left[\begin{array}{cc}3 & 2 \\ 5 & 1\end{array}\right] \cdot \left[\begin{array}{cc}x \\ v\end{array}\right] = \left[\begin{array}{cc}-1 \\ 3\end{array}\right] $
Formel 0-1: Aufgabe 2: Lösen Sie obiges Gleichungssystem erst von Hand und dann mit Hilfe von Scilab.
 Simulation eines linearen Feder-Masse-Dämpfer-Schwingers 54_Kinetik/01_Newton/04_ODE
Simulation eines linearen Feder-Masse-Dämpfer-Schwingers 54_Kinetik/01_Newton/04_ODE
ergänzendes Video:
 Modellerstellung und Simulation mit Scilab im Zeitbereich: 2020-11-24_11-05-30_RTS_Eulerintegration_ode.mp4
Modellerstellung und Simulation mit Scilab im Zeitbereich: 2020-11-24_11-05-30_RTS_Eulerintegration_ode.mp4
Dienstag 23.03.2021
|
Teil 1: Einführung in die Simulationstechnik
 Die Begriffe System und Modell -- 50_Simulationstechnik/01_Systemtheorie/01_System
Die Begriffe System und Modell -- 50_Simulationstechnik/01_Systemtheorie/01_System
 Modellierung von Mehrkörpersystemen -- 50_Simulationstechnik/01_Systemtheorie/02_Modell
Modellierung von Mehrkörpersystemen -- 50_Simulationstechnik/01_Systemtheorie/02_Modell
 Wann ist ein Modell gültig -- Verifikation -- 50_Simulationstechnik/01_Systemtheorie/03_Verifikation
Wann ist ein Modell gültig -- Verifikation -- 50_Simulationstechnik/01_Systemtheorie/03_Verifikation
 Modellbildung eines Seerosenteiches -- 50_Simulationstechnik/01_Systemtheorie/04_Seerosen
Modellbildung eines Seerosenteiches -- 50_Simulationstechnik/01_Systemtheorie/04_Seerosen
 Funktionen in Scilab -- 37_Scilab/03_Funktionen
Funktionen in Scilab -- 37_Scilab/03_Funktionen
 Einführung der Eulerintegration -- 50_Simulationstechnik/01_Systemtheorie/05_Eulerintegration
Einführung der Eulerintegration -- 50_Simulationstechnik/01_Systemtheorie/05_Eulerintegration
 "Saalübung" zum Seerosenteich -- 50_Simulationstechnik/01_Systemtheorie/06_Saaluebung
"Saalübung" zum Seerosenteich -- 50_Simulationstechnik/01_Systemtheorie/06_Saaluebung
 Scilabprogramm zum Seerosenteich -- 50_Simulationstechnik/01_Systemtheorie/07_scilab
Scilabprogramm zum Seerosenteich -- 50_Simulationstechnik/01_Systemtheorie/07_scilab
// erwartet wird: // 1Woche in Sekunden == 604800 // 6Mio == 10 Wochen // A0 == 20 // A10 == 20 * 2^10 = 20480, im Vergleich für deltaT=60 nur 19380 // Echte 10 Wochen gerechnet liefert: 20479.646 //Modell-Parameter k = 1/872542; deltat = 60; //deltat = 6; //um genauer zu werden!, liefert: 19383.458 t = 0; //n = 6000000; n = 6048000; //"Echte 10 Wochen" //Variablen und Anfangsbedingungen A0 = 20; A1 = 0; //Hilfsvariablen AA = A0; tt = 0; ii = 2; for i=0:deltat:n A1=k*A0*deltat + A0; A0 = A1; t = t + deltat; AA(ii) = A0; tt(ii) = t; ii=ii+1; end plot(tt,AA,'r-.+'); disp(A1);
Code 0-1: Eulerintegration des Seerosenteiches mit Scilab
function f = rechteSeite(t,y)
k = 1/872542;
A = y(1); // aktueller Systemzustand, hier Seerosenteichfläche
f(1) = k*A; // Funktion liefert aktuelle Steigung aus Systemzustand
endfunction
function y = eulerintegration(y0,t0,t,rechteSeite)
y = y0;
yalt = y0;
//Hilfsvariablen
tt = 0;
ii = 2;
deltat = t(2)-t(1);
zs = size(t);
spalten = zs(2);
for i=2:1:spalten
yneu=rechteSeite(t(i),yalt)*deltat + yalt;
yalt=yneu;
y(ii) = yneu;
ii=ii+1;
end
endfunction
y0 = 20;
t0 = 0;
t = 0:60:6048000;
y = eulerintegration(y0,t0,t,rechteSeite);
plot(t,y);
zs=size(y);
disp(y(zs(1)));
Code 0-2: Eulerintegration des Seerosenteiches mit Scilab aber indem für Modell und Integrator Funktionen definiert wurden.
Dienstag 30.03.2021
verschieben:
Vorübung:
|
Themen
 Eigenwertberechnung
Eigenwertberechnung
 Das Runge-Kutta-Integrationsverfahren -- 30_Informatik3/16_Nuetzliches/03_RungeKutta
Das Runge-Kutta-Integrationsverfahren -- 30_Informatik3/16_Nuetzliches/03_RungeKutta
 Implementierung des Runge-Kutta-Verfahrens -- 75_Echtzeit3/03_Processing/06_Snippets/15_Simulation
Implementierung des Runge-Kutta-Verfahrens -- 75_Echtzeit3/03_Processing/06_Snippets/15_Simulation
Teil 2: Einführung in die Modellbildung mechanischer Systeme
 Die Newton-Gleichung -- 54_Kinetik/01_Newton
Die Newton-Gleichung -- 54_Kinetik/01_Newton
 Modellierung eines linearen Schwingers -- 54_Kinetik/01_Newton/01_LinearSchwinger
Modellierung eines linearen Schwingers -- 54_Kinetik/01_Newton/01_LinearSchwinger
 Die Dämpfung / Dissipation von Energie -- 54_Kinetik/01_Newton/02_Daempfung
Die Dämpfung / Dissipation von Energie -- 54_Kinetik/01_Newton/02_Daempfung
 Verwendung des Integrators von Scilab -- 54_Kinetik/01_Newton/04_ODE
Verwendung des Integrators von Scilab -- 54_Kinetik/01_Newton/04_ODE
function f = rechteSeite(t,y) k = 1/872542; A = y(1); f(1) = k*A; endfunction clf; y0 = 20; t0 = 0; t = 0:60:6048000; y = ode(y0,t0,t,rechteSeite); plot(t,y); zs=size(y); letzte_spalte = zs(2); y(letzte_spalte)
Code 0-3: Seerosenteich mit ode integriert.
//Lösung Zuber clear; m = 1.0; C = 1.0; t = 0; n = 30; deltaT = 0.001; x=0; v=0; x0 = 1; v0 = 0; x_alt=x0; v_alt=v0; ii = 1; xxx=0; vvv=0; ttt=0; for i=0:deltaT:n // neu = alt + steigung*dt xxx(ii)=x_alt; vvv(ii)=v_alt; ttt(ii)=t; x = x_alt + v * deltaT; v = v_alt -(C/m) * x_alt * deltaT; //v = v_alt -(C/m) * x * deltaT; //numerisch stabiler x_alt = x; v_alt = v; t = t + deltaT; ii = ii+1; end clf; plot(ttt,xxx,'b',ttt,vvv,'r');
Code 0-4: Linearer Schwinger mit selbst geschriebenem Euler-Integrator ausgewertet (Studentische Lösung).
Dienstag 13.04.2021
Themen
|
Links zu den Themen auf kramann.info
 54_Kinetik/01_Newton/02_Daempfung
54_Kinetik/01_Newton/02_Daempfung
 62_Regelungssysteme/18_Fuzzy/09_Energie
62_Regelungssysteme/18_Fuzzy/09_Energie
 KOMMENDE WOCHE (vorschau): 54_Kinetik/05_Tilger
KOMMENDE WOCHE (vorschau): 54_Kinetik/05_Tilger
 50_Simulationstechnik/02_Eigenwerte/01_DGLS_Eigenwerte
50_Simulationstechnik/02_Eigenwerte/01_DGLS_Eigenwerte
 50_Simulationstechnik/02_Eigenwerte/02_scilab_Eigenwerte
50_Simulationstechnik/02_Eigenwerte/02_scilab_Eigenwerte
Übungen
 54_Kinetik/01_Newton/05_Saaluebung
54_Kinetik/01_Newton/05_Saaluebung
In der LV entstandene Scilab-Skripte
m = 1.0; C = 1.0; D = 1.0; function f = rechteSeite(t,y) A = [[-D/m,-C/m];[1,0]]; f = A*y; endfunction t = linspace(0,15,3000); y0 = [0,1]'; t0 = 0; y = ode(y0,t0,t,rechteSeite); //plot(t,y(1,:)',t,y(2,:)'); Eges=0.5.*C.*(y(2,:)').*(y(2,:)')+0.5.*m.*(y(1,:)').*(y(1,:)'); plot(t,Eges);
Code 0-5: Verlauf der Gesamtenergie bei Linearem Feder-Dämpfer-Masse-System
clear m=1; c=1; d=1; ii=0; function f= rechteSeite(t,y) x= y(1,1); v= y(2,1); f(1,1)=v; f(2,1)=-(c/m)*x-(d/m)*v; endfunction t=0:0.01:3; x0=[1,0]'; t0=0; y=ode(x0,t0,t,rechteSeite); //plot(t,y(1,:)',t,y(2,:)'); i=size(y(1,:)); //z=size(y(2,:)); E=0; for ii=1:1:i(2) E(ii)= (0.5)*m*(y(2,ii))^2+ (0.5)*c*(y(1,ii))^2; end plot(t,E);
Code 0-6: ... wie zuvor aber studentische Lösung unter Verwendung einer for-Schleife (ist weniger schnell in der Ausführung aber interessant wegen der alternativen Syntax).
Dienstag 20.04.2021
Themen
|
Übung
Ein linearer Feder-Masse-Schwinger habe die Masse 1kg und die Federkonstante C = 1 N/m. Wie muß die Dämpfung gewählt werden, damit die Eingefrequenz 1Hz beträgt?
Links zu den Themen
 von letzter Woche: 54_Kinetik/01_Newton/05_Saaluebung
von letzter Woche: 54_Kinetik/01_Newton/05_Saaluebung
 Technische Stabilität: 62_Regelungssysteme/07_Einstellregeln/05_Daempfungsgrad
Technische Stabilität: 62_Regelungssysteme/07_Einstellregeln/05_Daempfungsgrad
 Formel zu Zustandsregler: 62_Regelungssysteme/12_Adaptiv/06_Zustandsregler
Formel zu Zustandsregler: 62_Regelungssysteme/12_Adaptiv/06_Zustandsregler
 Auslegung eines Zustandsreglers: 62_Regelungssysteme/08_Polvorgabe
Auslegung eines Zustandsreglers: 62_Regelungssysteme/08_Polvorgabe
 Zustandsregler mit Beobachter (Vorschau): 62_Regelungssysteme/09_Beobachter
Zustandsregler mit Beobachter (Vorschau): 62_Regelungssysteme/09_Beobachter
neuere Darstellungen:
 80_Robuste_Systemintegration/01_Grundlagen/07_Zustandsregler
80_Robuste_Systemintegration/01_Grundlagen/07_Zustandsregler
 80_Robuste_Systemintegration/01_Grundlagen/08_Polvorgabe
80_Robuste_Systemintegration/01_Grundlagen/08_Polvorgabe
Saalübung
Folgendes System soll mit einem Zustandsregler versehen werden. Die Parameter des Zustandsreglers sollen so gewählt werden, dass das Gesamtsystem technisch stabil ist und die Eigenwerte des geregelten Systems bei Lambda = -1 +/- i liegen:
$ \ddot x = -x $
Formel 0-2: Zu regelndes System.
Übung
Wie zuvor, aber die neuen Eigenwerte sollen bei Lambda = -2 +/- 0.5*i liegen. Welche Eigenfrequenz hat dann das geregelte System?
Screenshots zur Einführung des Zustandsreglers:
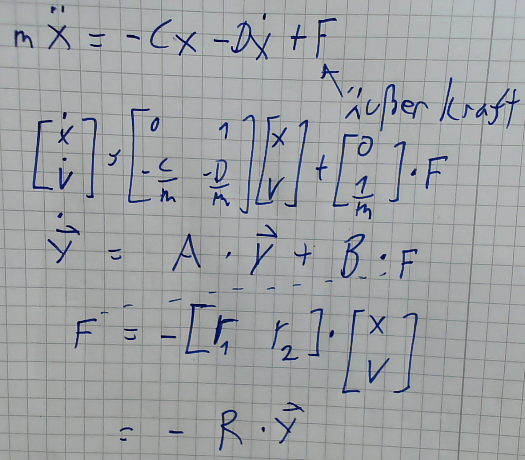
Bild 0-1: Herleitung Zustandsregler und Beispiel, Folie 1
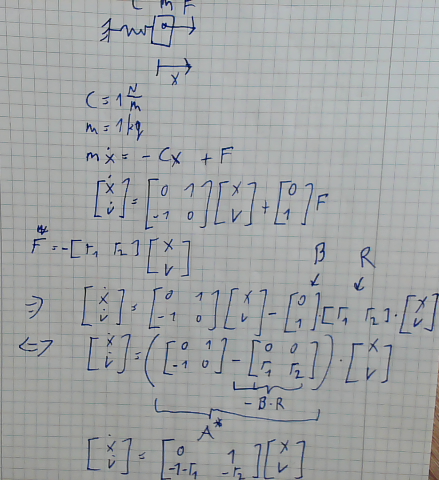
Bild 0-2: Herleitung Zustandsregler und Beispiel, Folie 2
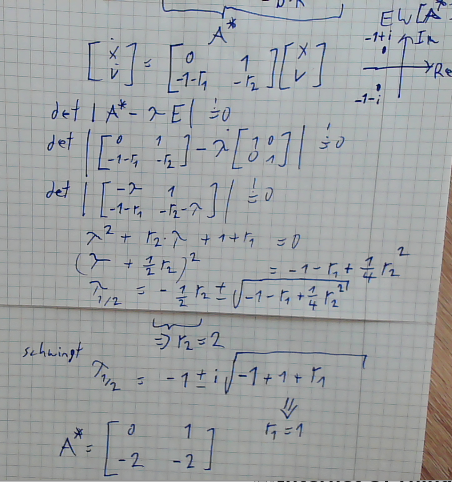
Bild 0-3: Herleitung Zustandsregler und Beispiel, Folie 3
Dienstag 27.04.2021
Literatur
|
Gehen Sie in eine Bibliothek mit einer konkreten Fragestellung und suchen Sie sich dasjenige Buch heraus, in dem diese am besten dargesetllt ist.
Themen
|
|
 80_Robuste_Systemintegration/01_Grundlagen/07_Zustandsregler
80_Robuste_Systemintegration/01_Grundlagen/07_Zustandsregler
 62_Regelungssysteme/04_Laplace
62_Regelungssysteme/04_Laplace
 62_Regelungssysteme/07_Einstellregeln/04_Scilab
62_Regelungssysteme/07_Einstellregeln/04_Scilab
 62_Regelungssysteme/01_day_by_day -- siehe 2 -- Dienstag 26.03.2019
62_Regelungssysteme/01_day_by_day -- siehe 2 -- Dienstag 26.03.2019
 62_Regelungssysteme -- siehe Themen Mittwoch, 25.03.2015
62_Regelungssysteme -- siehe Themen Mittwoch, 25.03.2015
später
 LDGLS in Übertragungsfunktion umwandeln und in Scilab simulieren: 2020-11-24_11-35-40_RTS_Uebertragungsfunktion_simulieren.mp4
LDGLS in Übertragungsfunktion umwandeln und in Scilab simulieren: 2020-11-24_11-35-40_RTS_Uebertragungsfunktion_simulieren.mp4
Übung 2
|
 62_Regelungssysteme/03_Verzoegerungsglieder
62_Regelungssysteme/03_Verzoegerungsglieder
 62_Regelungssysteme/04_Laplace
62_Regelungssysteme/04_Laplace
Aufgabe 3: Ein linearer Feder-Masse-Schwinger habe die Masse 1kg und die Federkonstante C = 1 N/m. Wie muß die Dämpfung gewählt werden, damit die Eingefrequenz 1Hz beträgt?
Beachte: Die Eigen-Kreisfrequenz(en) entspricht/entsprechen dem imaginären Anteil der Eigenwerte in einem linearen Differentialgleichungssystem (LDGLS).
clear;
function f = rechteSeite(t,y)
x = y(1,1);
v = y(2,1);
f(1,1) = v;
f(2,1) = -x-1.56*v;
endfunction
t = 0:0.1:100;
y0 = [1,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-7: Scilab-Code zur Simulation des Systems von Übung1, Aufgabe 3.
clear;
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[1+1.56*s+s^2]);
t=[0:0.01:100];
u=ones(1,10001);
y=csim(u,t,G);
plot2d(t,y);
Code 0-8: Scilab-Code zur Simulation des Systems von Übung1, Aufgabe 3 im Laplacebereich.
//s als Argument für ein Polynom definieren:
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[1+2*s+s^2]);
t=[0:0.01:10];
u=ones(1,1001);
y=csim(u,t,G);
plot2d(t,y);
//plzr(G);
Code 0-9: Übertragungsfunktionen beschreiben und auswerten mit Scilab.
|
|
 Hinweise zu Regelstrecken mit und ohne Ausgleich, sowie PT2-Übertragungsglied: 62_Regelungssysteme/03_Verzoegerungsglieder
Hinweise zu Regelstrecken mit und ohne Ausgleich, sowie PT2-Übertragungsglied: 62_Regelungssysteme/03_Verzoegerungsglieder
Aufgabe 3: Ein linearer Schwinger (m=1kg, C=1N/m) ohne Dämpfungselement wird mit einem aktiven Dämpfer ausgerüstet, also einem D-Element. Die Regeldifferenz zum Sollwert Null m/s wird mit Faktor 10 als äußere Kraft auf das System gegeben.
|
 Hinweise zu Laplace Transformationsregeln: 62_Regelungssysteme/04_Laplace
Hinweise zu Laplace Transformationsregeln: 62_Regelungssysteme/04_Laplace
Themen im letzten Teil:
|
 Methoden zur Eigenwertberechung: 62_Regelungssysteme/04_Laplace/01_Eigenwerte
Methoden zur Eigenwertberechung: 62_Regelungssysteme/04_Laplace/01_Eigenwerte
 Klassische Darstellung eines PID-Reglers: 62_Regelungssysteme/04_Laplace/04_Scilab
Klassische Darstellung eines PID-Reglers: 62_Regelungssysteme/04_Laplace/04_Scilab
 Plots mit Achsenbezeichnungen und Überschrift: 50_Simulationstechnik/01_Systemtheorie/07_scilab
Plots mit Achsenbezeichnungen und Überschrift: 50_Simulationstechnik/01_Systemtheorie/07_scilab
 Gesamtübertragungsverhalten geschlossener Regelkreis (Laplace): 62_Regelungssysteme/04_Laplace/03_PRegler
Gesamtübertragungsverhalten geschlossener Regelkreis (Laplace): 62_Regelungssysteme/04_Laplace/03_PRegler
Dienstag 04.05.2021
Übung
Transformieren Sie in den Laplace-Bereich:
$ \ddot x = -x + u $
Formel 0-3: Formel 1.
$ \ddot x = -x - \dot x + u $
Formel 0-4: Formel 2.
$ \ddot x = -x - \dot x + u + \dot u $
Formel 0-5: Formel 3.
Transformieren Sie in den Laplace-Bereich und berücksichtigen Sie beide Gleichungen gemeinsam:
$ \ddot x = -x - \dot x + F $
Formel 0-6: Formel 4.
$ F = 5 \cdot \left(w-x\right) $
Formel 0-7: Formel 5.
Hierbei handelt es sich um einen P-Regler mit Verstärkungsfaktor 5, der in die Regelstrecke eingebaut wurde.
Eine Umsetzung und Simulation im Zeitbereich und im Laplacebereich genau dieses Systems erfolgt nachfolgend:
clear;
// x.. = -x -x. +F
// F = 5*(w-x)
function f = rechteSeite(t,y)
x = y(1,1);
v = y(2,1);
w = 2;
F = 5*(w-x); //P-Regler
f(1,1) = v;
f(2,1) = -x-v+F;
endfunction
t = 0:0.1:15;
y0 = [0,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-10: Umsetzung im Zeitbereich.
clear;
//s als Argument für ein Polynom definieren:
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[s^2+s+1]); //Regelstrecke, Input:F, Output:x
R = syslin('c',[5],[1]); //Regler, Input:e=(w-x), Output:F
Q = R*G;//Gesamtübertragungsverhalten des offenen Regelkreises
//Input:e, Output:x
H = Q/(1+Q); //Gesamtü. geschl. RK, Input:w, Output:x
//H = syslin('c',[5],[s^2+s+6]);
t = 0:0.1:15;
zs=size(t);
w=2*ones(1,zs(2));
y=csim(w,t,H);
plot(t,y,'r--');
Code 0-11: Umsetzung im Laplace-Bereich.
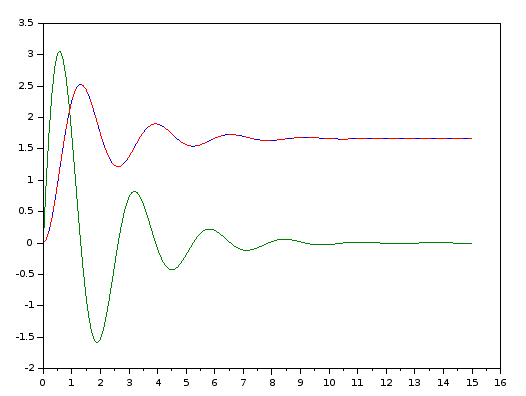
Bild 0-4: Übereinandergelegte Plots: Laplace rot, Zeitbereich blau für die Auslenkung x.
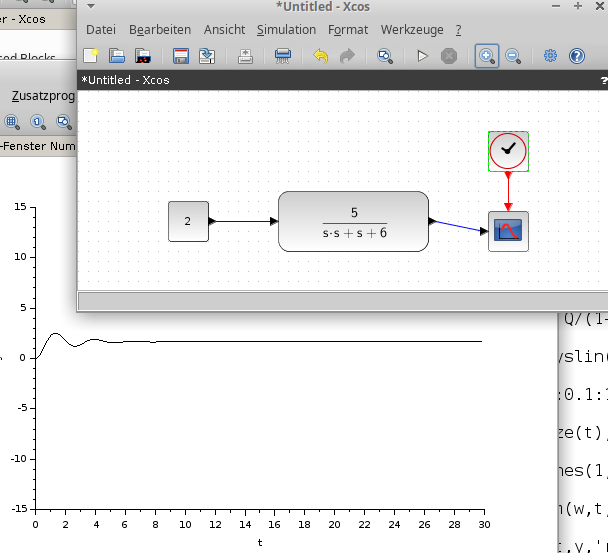
Bild 0-5: Umsetzung des gleichen Systems mittels xcos in Scilab (Pendant zu Simulink in Matlab).
Transformieren Sie in den Zeitbereich, Input sei u, Output sein y:
$ G\left(s\right) = \frac {1}{s^2+s} $
Formel 0-8: Formel 6.
$ G\left(s\right) = \frac {1+s}{s^2+s} $
Formel 0-9: Formel 7.
Transformieren Sie Q(s)und H(s) jeweils in den Zeitbereich, Input sei u, Output sein y. Berücksichtigen Sie alle Gleichungen:
$ G\left(s\right) = \frac {1}{s^2+2 \cdot s+1} $
Formel 0-10: Formel 8.
$ R\left(s\right) = \frac {s \cdot 3+1}{1} $
Formel 0-11: Formel 9.
$ Q\left(s\right) = R\left(s\right) \cdot G\left(s\right) $
Formel 0-12: Formel 10.
$ H\left(s\right) = \frac {Q\left(s\right)}{1+Q\left(s\right)} $
Formel 0-13: Formel 11 -- geschlossener Regelkreis.
Überlegen Sie für jedes Element eines geschlossenen Regelkreises, was dort jeweils Eingang und was Ausgang ist: Regelstrecke G(s), Regler R(s), offener Regelkreis Q(s)=R(s)*G(s), geschlossener Regelkreis H(s)=Q(s)/(1+Q(s)).
Themen
|
 siehe dazu: 62_Regelungssysteme/04_Laplace/03_PRegler
siehe dazu: 62_Regelungssysteme/04_Laplace/03_PRegler
|
 Beispiel hierzu: 62_Regelungssysteme/04_Laplace/04_Scilab
Beispiel hierzu: 62_Regelungssysteme/04_Laplace/04_Scilab
 siehe auch "Zu Übung 2, Aufgabe 3 von letzter Woche: " hier: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21
siehe auch "Zu Übung 2, Aufgabe 3 von letzter Woche: " hier: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21
 syslin: siehe "Code 0-2: Feder-Masse-Schwinger mit äußerer Kraft F im Zeit- und Laplacebereich simulieren. " in 62_Regelungssysteme/01_day_by_day
syslin: siehe "Code 0-2: Feder-Masse-Schwinger mit äußerer Kraft F im Zeit- und Laplacebereich simulieren. " in 62_Regelungssysteme/01_day_by_day
Dienstag 11.05.2021
Themen
|
Übung: Quiz (erst 20 Min. allein oder in kleinen Gruppen, dann gemeinsam)
|
Links zum Thema PID-Regler
 62_Regelungssysteme/04_Laplace/04_Scilab -- Struktur eines PID-Reglers
62_Regelungssysteme/04_Laplace/04_Scilab -- Struktur eines PID-Reglers
 62_Regelungssysteme/07_Einstellregeln -- Reglerauslegungsmethoden nach Ziegler und Nichols, für: P-, PI- und PID-Regler.
62_Regelungssysteme/07_Einstellregeln -- Reglerauslegungsmethoden nach Ziegler und Nichols, für: P-, PI- und PID-Regler.
 62_Regelungssysteme/05_Regleroptimierung/03_Scilab -- PID-Regler im Zeitbereich, siehe "Darstellung des Gesamtmodells im Zeitbereich und Optimierung mit Scilab"
62_Regelungssysteme/05_Regleroptimierung/03_Scilab -- PID-Regler im Zeitbereich, siehe "Darstellung des Gesamtmodells im Zeitbereich und Optimierung mit Scilab"
 62_Regelungssysteme -- siehe Themen Mittwoch, 13.05.2015, PID-Regler im Zeitbereich: Hinzufügen des I-Anteils in Scilab.
62_Regelungssysteme -- siehe Themen Mittwoch, 13.05.2015, PID-Regler im Zeitbereich: Hinzufügen des I-Anteils in Scilab.
Darstellung: R(s) = s + 1 + 1/s, G(s)=s*s+1.
Übung
|
Während des Unterrichts entstandene Scilab-Quelltexte
clear;
//s als Argument für ein Polynom definieren:
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[s*s+0.1]); //Regelstrecke, Input:F, Output:x
// R = K*(1 + 1/(Tn*s) + Tv*s)
// R = 0.5*(1 + 1/(10*s) + 0.1*s)
// geändert: K=10
// R = 10*(1 + 1/(10*s) + 0.1*s)
// R = 10 + 1/s + s
// R = (10*s + 1 + s^2) / s
//R = syslin('c',[ZÄHLER],[NENNER]);
R = syslin('c',[s*s+10.0*s+1.0],[1.0*s]); // PI-Regler, Input:e=(w-x), Output:F
/*R(s)=(s^2 + 10s +1)/s
= s + 10 +1/s
= 10(1 + 1/(10*s) + 0.1*s )
K = 10 (von 0.5 auf 10)
T_N = 10
T_v = 0.1
*/
//R = syslin('c', [0.5+0.05*s], [1]); //K = 0.5, T_v=0.1
//R = syslin ('c', [10 + s], [1]); // K =10, T_v = 0.1
Q = R*G;//Gesamtübertragungsverhalten des offenen Regelkreises
//Input:e, Output:x
H = Q/(1+Q); //Gesamtü. geschl. RK, Input:w, Output:x
t = 0:0.1:15;
zs=size(t);
w=2*ones(1,zs(2));
y=csim(w,t,H);
plot(t,y,'r');
Code 0-12: Studentische Lösung
clear;
//s als Argument für ein Polynom definieren:
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[s^2+s+1]); //Regelstrecke, Input:F, Output:x
//R = syslin('c',[5],[1]); //Regler, Input:e=(w-x), Output:F
//... daraus einen PI-Regler machen!:
//ZU SCHWACH:
// R = 5 + 0.1/s ... Hauptnenner:
// = (5*s + 0.1) / s
// **** NEW *** NEW *** NEW ***
// Regeldifferenz e wird nun nicht mehr nur proportional verstärkt,
// sondern auch dazu (Addition) noch integriert über die Zeit:
//R = syslin('c',[5*s+0.1],[s]); // PI-Regler, Input:e=(w-x), Output:F
//STÄRKER:
// R = 5 + 1.5/s ... Hauptnenner:
// = (5*s + 1.5) / s
// **** NEW *** NEW *** NEW ***
// Regeldifferenz e wird nun nicht mehr nur proportional verstärkt,
// sondern auch dazu (Addition) noch integriert über die Zeit:
R = syslin('c',[5.0*s+1.5],[s]); // PI-Regler, Input:e=(w-x), Output:F
Q = R*G;//Gesamtübertragungsverhalten des offenen Regelkreises
//Input:e, Output:x
H = Q/(1+Q); //Gesamtü. geschl. RK, Input:w, Output:x
//H = syslin('c',[5],[s^2+s+6]);
t = 0:0.1:15;
zs=size(t);
w=2*ones(1,zs(2));
y=csim(w,t,H);
plot(t,y,'r');
Code 0-13: PI-Regler
Dienstag 18.05.2021
Themen
|
Links zu den Unterrichtsthemen
 30_Informatik3/16_Nuetzliches/03_RungeKutta
30_Informatik3/16_Nuetzliches/03_RungeKutta
 62_Regelungssysteme/07_Einstellregeln/01_Totzeit
62_Regelungssysteme/07_Einstellregeln/01_Totzeit
 62_Regelungssysteme/07_Einstellregeln/02_Methode1
62_Regelungssysteme/07_Einstellregeln/02_Methode1
Übung
|
Scilab-Quelltexte im Zusammenhang mit obiger Übung
clear();
xtot=0;
function f=modell(y,t,dt)
x=y(1,1);
v=y(2,1);
Kkrit = 2.21;
xsoll = 1.0;
//e = xsoll - x;
e = xsoll - xtot;
u=Kkrit*e;
f(1,1)=v;
f(2,1)=-x-v+u;
endfunction
function yneu=ruku(y,t,dt)
k1=modell(y,t,dt);
k2=modell(y+0.5.*dt.*k1,t+0.5*dt);
k3=modell(y+0.5.*dt.*k2,t+0.5*dt);
k4=modell(y+dt.*k3,t+dt);
yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6;
endfunction
tmax = 60.0;
dt = 0.01;
schritte = ceil(tmax/dt);
yalt = [0,0]';
ysim = yalt;
t=0.0;
tt=t;
Ttot = 0.5;
anztot = round(Ttot/dt)
xtotarr = zeros(anztot,1);
for i=1:1:schritte
yneu=ruku(yalt,t,dt);
yalt=yneu;
ysim=[ysim,yalt];
tt =[tt,t];
t=t+dt;
xtot = xtotarr(modulo((i-1),anztot)+1);
xtotarr(modulo((i-1),anztot)+1)=yneu(1);
end
plot(tt,ysim(1,:))
Code 0-14: Einführen einer Totzeit von 0,5 Sekunden und Einbau eines P-Reglers, um Kkrit zu finden.
kill(all); R : 9.7*(1+1/(0.5*1.97*s)+ 0.12*1.97*s);
Code 0-15: Verwenden von Maxima, um Zähler und Nenner einer Übertragungsfunktion zu finden (studentische Lösung)
s = poly(0,"s");
//R = syslin('c',[0.5*9.7],[1]);
G = syslin('c',[1],[s*s+s+1]);
R = syslin('c',[11293419*s*s+47772500*s+48500000],[4925000*s]);
Q = R * G;
H = Q/(1+Q);
t = 0:0.1:60;
zs=size(t);
w=1*ones(1,zs(2));
y=csim(w,t,H);
Code 0-16: Verwendung der mit Maxima gefundenen Übertragungsfunktion (studentische Lösung).
//Musterlösung zur Übung
clear();
xtot=0;
function f=modell(y,t,dt)
x=y(1,1);
v=y(2,1);
Kkrit = 9.7; //#### ANGEPASST ####
xsoll = 1.0;
//e = xsoll - x;
e = xsoll - xtot;
u=Kkrit*e;
f(1,1)=v;
f(2,1)=-x-v+u; //#### gleiche Regelstrecke! ####
endfunction
function yneu=ruku(y,t,dt)
k1=modell(y,t,dt);
k2=modell(y+0.5.*dt.*k1,t+0.5*dt);
k3=modell(y+0.5.*dt.*k2,t+0.5*dt);
k4=modell(y+dt.*k3,t+dt);
yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6;
endfunction
tmax = 60.0;
dt = 0.01;
schritte = ceil(tmax/dt);
yalt = [0,0]';
ysim = yalt;
t=0.0;
tt=t;
Ttot = 0.1; // #### ANGEPASST ####
anztot = round(Ttot/dt)
xtotarr = zeros(anztot,1);
for i=1:1:schritte
yneu=ruku(yalt,t,dt);
yalt=yneu;
ysim=[ysim,yalt];
tt =[tt,t];
t=t+dt;
xtot = xtotarr(modulo((i-1),anztot)+1);
xtotarr(modulo((i-1),anztot)+1)=yneu(1);
end
plot(tt,ysim(1,:))
Code 0-17: MUSTERLÖSUNG ZUR ÜBUNG
//Musterlösung zur Übung zweiter Teil!
clear();
//Laut Tabelle für PID:
Kkrit = 9.7;
Tkrit = 1.97;
K = Kkrit*0.6;
TN = Tkrit*0.5;
TV = Tkrit*0.12;
// R(s) = K*(1+1/(TN*s)+TV*s)
// R(s) = K + K/(TN*s) + K*TV*s ### Klammer aufgelöst
// R(s) = (K*TN*s + K + K*TN*TV*s^2) / (TN*s)
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[s^2+s+1]); //Regelstrecke, Input:F, Output:x
R = syslin('c',[K*TN*s + K + K*TN*TV*s^2],[TN*s]);
Q = R*G;//Gesamtübertragungsverhalten des offenen Regelkreises
H = Q/(1+Q); //Gesamtü. geschl. RK, Input:w, Output:x
t = 0:0.1:15;
zs=size(t);
w=1*ones(1,zs(2));
y=csim(w,t,H);
plot(t,y,'r');
Code 0-18: MUSTERLÖSUNG ZUR ÜBUNG (2. Teil)
clear();
//Musterlösung zur Übung
// PID-Regler im Zeitbereich formulieren!!!
//Laut Tabelle für PID:
//Frage: Liegen die Eigenwerte des kritischen Systems auf der imaginären Achse?
Kkrit = 9.7;
Tkrit = 1.97;
K = Kkrit*0.6;
TN = Tkrit*0.5;
TV = Tkrit*0.12;
// R(s) = K*(1+1/(TN*s)+TV*s)
// PID-Regler im Zeitbereich:
// u = K*e + (K/TN)* Integral_e + (K*TV)*(de/dt)
xtot=0;
vtot=0;
function f=modell(y,t,dt)
x=y(1,1);
v=y(2,1);
einteg = y(3,1); //dritter Zustand ist gerade das Integral der Regeldifferenz
Kkrit = 9.7; //#### ANGEPASST ####
xsoll = 1.0;
//e = xsoll - x;
e = xsoll - xtot;
ediff = 0 - vtot;
//einteg = ??????
// de/dt = -vtot, wenn xsoll als konstant angenommen wird!
// u = K*e + (K/TN)* Integral_e + (K*TV)*(de/dt)
u=K*e + (K/TN)*einteg + (K*TV)*(ediff);
f(1,1)=v;
f(2,1)=-x-v+u; //#### gleiche Regelstrecke! ####
f(3,1)=e; //Ableitung des dritten Zustandes ist dann e
endfunction
function yneu=ruku(y,t,dt)
k1=modell(y,t,dt);
k2=modell(y+0.5.*dt.*k1,t+0.5*dt);
k3=modell(y+0.5.*dt.*k2,t+0.5*dt);
k4=modell(y+dt.*k3,t+dt);
yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6;
endfunction
tmax = 60.0;
dt = 0.01;
schritte = ceil(tmax/dt);
yalt = [0,0,0]';
ysim = yalt;
t=0.0;
tt=t;
Ttot = 0.1; // #### ANGEPASST ####
anztot = round(Ttot/dt)
xtotarr = zeros(anztot,1);
vtotarr = zeros(anztot,1);
for i=1:1:schritte
yneu=ruku(yalt,t,dt);
yalt=yneu;
ysim=[ysim,yalt];
tt =[tt,t];
t=t+dt;
xtot = xtotarr(modulo((i-1),anztot)+1);
xtotarr(modulo((i-1),anztot)+1)=yneu(1);
vtot = vtotarr(modulo((i-1),anztot)+1);
vtotarr(modulo((i-1),anztot)+1)=yneu(2);
end
plot(tt,ysim(1,:))
Code 0-19: MUSTERLÖSUNG ZUR ÜBUNG (PID im Zeitbereich formulieren, dazu: 3. Systemzustand Integral der Regeldifferenz einführen).
Dienstag 25.05.2021
Themen
|
Bitte beachten Sie die Klausurtermine auf der Startseite von kramann.info
|
| Autor | Titel | erschienen bei | Hinweise |
|---|---|---|---|
| Zacher, S., Reuter, M. | Regelungstechnik für Ingenieure | Springer, Wiesbaden, 2008 | Zustandsregler und auch Neuro- und Fuzzy-Regler werden u.a. behandelt |
| Beater, P. | Regelungstechnik und Simulationstechnik mit Scilab und Modelica: Eine beispielorientierte Einführung für Studenten und Anwender aus dem Maschinenbau | Books on Demand, 2010 | Verwendung von Scilab. |
Tabelle 0-1: Literatur zu Regelungstechnik
 15_Einachser -- Motivation: Einachser mit Arduino und modifizierten Modellbauservos.
15_Einachser -- Motivation: Einachser mit Arduino und modifizierten Modellbauservos.
 02_WS2020_21/01_RTS/01_day_by_day -- siehe Tafelbilder bei "Musterlösung zu Übung 2 vom 15.12.2020".
02_WS2020_21/01_RTS/01_day_by_day -- siehe Tafelbilder bei "Musterlösung zu Übung 2 vom 15.12.2020".
Übung
|
clear; m = 1.0; l = 1.0; h = 0.5; r = 0.1; g = 9.81; J = 1/4 * m* r*r + 1/12 * m * l*l; x_A = 0; /* m xpp = F_A m ypp = F_y - F_g J phipp = F_y*h*sin(phi) + F_A*h*cos(phi) */ function phi_punkt = rechteSeite(t,y) phi=y(1,1); xsi=y(2,1); // F_A = 0; //P-Regler: F_A = K(w-phi); w=0 grad K = 10; F_A = -K*phi; // x = y(3,1); // v... phi_punkt(1,1) = xsi phi_punkt(2,1) =(m*g*h*sin(phi)-m*h*h*xsi*xsi*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi)); endfunction t = 0:0.1:15; y0 = [10.0*%pi/180,0.0]'; t0 = 0; y = ode(y0,t0,t,rechteSeite); clf; plot(t,y(1,:)');
Code 0-20: Studentische Lösung der Übung.
Dienstag 01.06.2021
Themen: Fortsetzung invertierendes Pendel
|
Quiz
|
Formulierung der heutigen Themen als Übungen mit Nachbesprechung:
Hinweis zur Reglerauslegung:
|
|
 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, PREVIEW Zustandsregler für invertierendes Pendel bzgl. phi, siehe: Musterlösung zu Übung 2 vom 15.12.2020
62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, PREVIEW Zustandsregler für invertierendes Pendel bzgl. phi, siehe: Musterlösung zu Übung 2 vom 15.12.2020
|
|
Es macht Sinn, die Ergebnisse zu animieren. Hier ein Beispiel zu einer möglichen Umsetzung:
 Quelle: http://www.kramann.info/02_WS2020_21/01_RTS/01_day_by_day/index.php
Quelle: http://www.kramann.info/02_WS2020_21/01_RTS/01_day_by_day/index.php
clear; dt=0.1; t = 0:dt:100; zs = size(t); zeilen = zs(1); spalten = zs(2); // Punkt A: [x;y] zeitlicher Verlauf == [0;0] pA = zeros(2,spalten); // Punkt B: [x;y] zeitlicher Verlauf == [sin(...);1] pB = [sin(2*%pi*0.2*t);ones(1,spalten)]; //Eine Animation soll eine Verbindungslinie von pA mit pB im zeitlichen Verlauf darstellen: isoview; clf; // ABBRUCH MIT CTR C !! for i=1:spalten clf; plot([-2,-1.999,1.999,2],[0,2,2,0]); //Rahmen, um Skalierung konstant zu halten plot([pA(1,i),pB(1,i)],[pA(2,i),pB(2,i)]); sleep(1000*dt); // "Echtzeit" end
Code 0-21: Animation mit Scilab.
Themen 2. Vorlesung Regelungstechnik, u.a.:
|
Studentische Lösungen
clear; // phi_pp= 1/J * (h*m*g*phi+ h * F_A) // phi_pp = phi * h*m*g/J + F_A * h/J m = 1; m = 1.0; l = 1.0; h = 0.5; r = 0.1; g = 9.81; J = 1/4 * m* r*r + 1/12 * m * l*l; //phi_p = xsi; //xsi_p = phi * mgh/J + F_A*h/J A = [0 1; m*g*h/J, 0] //A*y = A*[phi;xsi] B = [0; h/J] //B*R oder B*u oder B*F_A lambda = spec(A) //+- 7,559 = instabil EW = [-1+%i;-1-%i] R = ppol(A,B,EW) // A_stern = A-B*R //B*R = B * R *[phi;xsi] spec(A_stern)
Code 0-22: Bestimmung der Regelmatrix R
Benutzung der Regelmatrix:
clear; m = 1.0; l = 1.0; h = 0.5; r = 0.1; g = 9.81; J = 1/4 * m* r*r + 1/12 * m * l*l; A = [0 1; m*g*h/J, 0]; B = [0; h/J]; EW = [-1+%i;-1-%i]; R = ppol(A,B,EW); A_stern = A-B*R spec(A_stern); function ydot = rechteSeite(t,y) phi=y(1,1); xsi=y(2,1); F_A = -R*[phi;xsi]; ydot(1,1) = xsi ydot(2,1) =(m*g*h*sin(phi)-m*h*h*xsi*xsi*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi)); endfunction t = linspace(0,20,3000); y0 = [0.2,0.1]'; //angabe der Winkel-v t0 = 0; y = ode(y0,t0,t,rechteSeite); clf; plot(t,y(1,:)',t,y(2,:)');
Code 0-23: Simulation des geregelten Systems
... mit Zustand x und Animation
clear; m = 1.0; l = 1.0; h = 0.5; r = 0.1; g = 9.81; J = 1/4 * m* r*r + 1/12 * m * l*l; A = [0 1; m*g*h/J, 0]; B = [0; h/J]; EW = [-1+%i;-1-%i]; R = ppol(A,B,EW); A_stern = A-B*R spec(A_stern); function ydot = rechteSeite(t,y) phi=y(1,1); xsi=y(2,1); x =y(3,1); vx =y(4,1); F_A = -R*[phi;xsi]; ydot(1,1) = xsi ydot(2,1) =(m*g*h*sin(phi)-m*h*h*xsi*xsi*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi)); ydot(3,1) = vx; // x. = v ydot(4,1) = F_A/m; // m*x.. = FA => x.. = v. = FA/m ... Newton-Gleichung in x-Richtung endfunction t = linspace(0,20,3000); dt = 20/3000; //y0 = [0.2,0.1,0,0]'; //angabe der Winkel-v y0 = [0.5,0.0,0,0]'; //angabe der Winkel-v t0 = 0; y = ode(y0,t0,t,rechteSeite); clf; plot(t,y(1,:)',t,y(2,:)'); // Für eine Animation benötigen wir die Endpunkte es Stabes in ihrer Bewegung // Wir könnten dann die Verbindungslinie dieser Endpunkte A-B über die Zeit zeigen. // Wie berechnen wir diese Endpunkte? // 1. Bestimmung von ys (y des Schwerpunktes): ys = h * cos(phi) ... "siehe Tafelbild" phi = y(1,:); ys = h * cos(phi); xs = y(3,:); // 2. Bestimmung von punktA = punktS + rSA, punktB = punktS - rSA ... siehe Tafelbild xA = xs + h*sin(phi); yA = ys - h*cos(phi); xB = xs - h*sin(phi); yB = ys + h*cos(phi); pA = [xA;yA]; pB = [xB;yB]; //Eine Animation soll eine Verbindungslinie von pA mit pB im zeitlichen Verlauf darstellen: isoview; clf; // ABBRUCH MIT CTR C !! zeilenspalten = size(pA); spalten = zeilenspalten(2); for i=1:spalten clf; plot([-2,-1.999,1.999,2],[-2,2,2,-2]); //Rahmen, um Skalierung konstant zu halten plot([pA(1,i),pB(1,i)],[pA(2,i),pB(2,i)]); sleep(1000*dt); // "Echtzeit" end
Code 0-24: ... mit Animation.
Simulation und Animation des ungeregelten Pendels.
clear; m = 1.0; l = 1.0; h = 0.5; r = 0.1; g = 9.81; J = 1/4 * m* r*r + 1/12 * m * l*l; A = [0 1; m*g*h/J, 0]; B = [0; h/J]; EW = [-1+%i;-1-%i]; R = ppol(A,B,EW); A_stern = A-B*R spec(A_stern); function ydot = rechteSeite(t,y) phi=y(1,1); xsi=y(2,1); x =y(3,1); vx =y(4,1); //F_A = -R*[phi;xsi]; F_A = 0; ydot(1,1) = xsi ydot(2,1) =(m*g*h*sin(phi)-m*h*h*xsi*xsi*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi)); ydot(3,1) = vx; // x. = v ydot(4,1) = F_A/m; // m*x.. = FA => x.. = v. = FA/m ... Newton-Gleichung in x-Richtung endfunction t = linspace(0,20,3000); dt = 20/3000; y0 = [0.2,0.1,0,0]'; //angabe der Winkel-v t0 = 0; y = ode(y0,t0,t,rechteSeite); clf; plot(t,y(1,:)',t,y(2,:)'); // Für eine Animation benötigen wir die Endpunkte es Stabes in ihrer Bewegung // Wir könnten dann die Verbindungslinie dieser Endpunkte A-B über die Zeit zeigen. // Wie berechnen wir diese Endpunkte? // 1. Bestimmung von ys (y des Schwerpunktes): ys = h * cos(phi) ... "siehe Tafelbild" phi = y(1,:); ys = h * cos(phi); xs = y(3,:); // 2. Bestimmung von punktA = punktS + rSA, punktB = punktS - rSA ... siehe Tafelbild xA = xs + h*sin(phi); yA = ys - h*cos(phi); xB = xs - h*sin(phi); yB = ys + h*cos(phi); pA = [xA;yA]; pB = [xB;yB]; //Eine Animation soll eine Verbindungslinie von pA mit pB im zeitlichen Verlauf darstellen: isoview; clf; // ABBRUCH MIT CTR C !! zeilenspalten = size(pA); spalten = zeilenspalten(2); for i=1:spalten clf; plot([-2,-1.999,1.999,2],[-2,2,2,-2]); //Rahmen, um Skalierung konstant zu halten plot([pA(1,i),pB(1,i)],[pA(2,i),pB(2,i)]); sleep(1000*dt); // "Echtzeit" end
Code 0-25: Simulation und Animation des ungeregelten Pendels.
Bild 0-6: Screenshot der Animation.
Dienstag 08.06.2021
Themen
|
 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, siehe ab "Musterlösung zu Übung 2 vom 15.12.2020"
62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, siehe ab "Musterlösung zu Übung 2 vom 15.12.2020"
 62_Regelungssysteme/11_Stabilitaet/03_Windup
62_Regelungssysteme/11_Stabilitaet/03_Windup
 62_Regelungssysteme/05_Regleroptimierung/07_Stoerverhalten
62_Regelungssysteme/05_Regleroptimierung/07_Stoerverhalten
Entwurf und Simulation mit Zustandsregler für x und phi:
clear;
//Parameter:
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
//Auslegung des Zustandsreglers,
//der den Gesamtzustand ausregeln soll,
// also so, dass phi und x nach und
// nach zu Null werden, wobei phi
// schneller ausgeregelt werden soll.
A = [0 1 0 0
(m*g*h)/J 0 0 0
0 0 0 1
0 0 0 0];
B = [0; h/J; 0; 1/m];
q=7.5594729;
r=1.0;
EW = [-q+q*%i,-q-q*%i,-r+r*%i,-r-r*%i];
R = ppol(A,B,EW)
Astern = A - B*R;
spec(Astern)
//------------------------
//Simulation mit NICHT-linearisiertem
// System, aber mit dem
//aus der linearisierten Betrachtung
//gewonnenen Zustandsregler:
function ydot = rechteSeite(t,y)
phi=y(1,1);
xsi=y(2,1);
x =y(3,1);
vx =y(4,1);
//F_A = -R*[phi;xsi];
F_A = -R*[phi;xsi;x;vx];
//F_A = 0;
ydot(1,1) = xsi
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*xsi*xsi*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
ydot(3,1) = vx; // x. = v
ydot(4,1) = F_A/m; // m*x.. = FA => x.. = v. = FA/m ... Newton-Gleichung in x-Richtung
endfunction
t = linspace(0,20,3000);
dt = 20/3000;
y0 = [0.2,0.1,0,0]'; //angabe der Winkel-v
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
clf;
plot(t,y(1,:)',t,y(2,:)');
// Für eine Animation benötigen wir die Endpunkte es Stabes in ihrer Bewegung
// Wir könnten dann die Verbindungslinie dieser Endpunkte A-B über die Zeit zeigen.
// Wie berechnen wir diese Endpunkte?
// 1. Bestimmung von ys (y des Schwerpunktes): ys = h * cos(phi) ... "siehe Tafelbild"
phi = y(1,:);
ys = h * cos(phi);
xs = y(3,:);
// 2. Bestimmung von punktA = punktS + rSA, punktB = punktS - rSA ... siehe Tafelbild
xA = xs + h*sin(phi);
yA = ys - h*cos(phi);
xB = xs - h*sin(phi);
yB = ys + h*cos(phi);
pA = [xA;yA];
pB = [xB;yB];
//Eine Animation soll eine Verbindungslinie von pA mit pB im zeitlichen Verlauf darstellen:
isoview;
clf;
// ABBRUCH MIT CTR C !!
zeilenspalten = size(pA);
spalten = zeilenspalten(2);
for i=1:spalten
clf;
plot([-2,-1.999,1.999,2],[-2,2,2,-2]); //Rahmen, um Skalierung konstant zu halten
plot([pA(1,i),pB(1,i)],[pA(2,i),pB(2,i)]);
sleep(1000*dt); // "Echtzeit"
end
Code 0-26: Entwurf und Simulation mit Zustandsregler für x und phi:
Übung
Jetzt 60Min Übung: I-Anteil beim linearisierten Pendel mit phi, omega ergänzen, also Integral von phi und für diese neue Systemmatrix einen Zustandsregler finden und mit der Lösung ohne I-Anteil qualitativ vergleichen.
clear();
m = 1; //kg
g = 0.91; // m/s^2
l = 1; // m
h = l/2; // m
r = 0.1; // m
// siehe: http://www.kramann.info/54_Kinetik/02_NewtonEuler/01_Traegheitsmomente
J = 0.25*m*r*r + (1/12)*m*l*l; // kg*m^2
//Einführen eines fiktiven Zustandes phi_integ = Integral phi dt,
//oder: d phi_integ / dt = phi (Die Ableitung dieses Zustandes ergibt phi)
A = [ 0 , 1 , 0 ;
m*g*h/J , 0 , 0 ;
1 , 0 , 0 ];
B = [ 0 ; h/J ; 0 ];
spec(A) //Eigenwerte der ursprünglichen Matrix ansehen
// ergibt:
// 0. + 0.i
// 2.3023837 + 0.i
// -2.3023837 + 0.i
// technisch stabil wählen, an vorhandenen Werten orientieren:
// Der dritte Eigenwert kann nur real sein!
EW = [-2.3023837 + %i*2.3023837 , -2.3023837 - %i*2.3023837 , -2.3023837];
R = ppol(A,B,EW)
// 4.5499999 1.1857276 4.1903382
//testweise diesen Regler in das nicht linearisierte Modell einbauen und testen:
function f = rechteSeite(t,y)
phi = y(1,1);
om = y(2,1);
phi_integ = y(3,1);
f(1,1) = om;
FA = -R * [phi;om;phi_integ];
N = J + m*h*h*sin(phi)*sin(phi);
f(2,1) = (-m*h*h*om*om*sin(phi)*cos(phi) + h*m*sin(phi)*g + h*cos(phi)*FA )/N;
f(3,1) = phi;
endfunction
t = linspace(0,20,3000);
y0 = [10.0*%pi/180,0.0,0.0]'; //Start in der Nähe der instabilen Ruhelage
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-27: Musterlösung zur obigen Übung.
Dienstag 15.06.2021
Themen
|
 62_Regelungssysteme/05_Regleroptimierung/07_Stoerverhalten
62_Regelungssysteme/05_Regleroptimierung/07_Stoerverhalten
In der letzten Woche tauchte bei dem Versuch einen Zustandsregler mit ppol in Scilab auszulegen, der ergänzend integrative Zustände für phi und x erhalten hatte die Meldung auf: ppol: Uncontrollable system
Steuerbarkeit
"Uncontrollable" ist ein lineares System, wenn es nicht steuerbar ist.
Steuerbarkeit: Ein System ist steuerbar, wenn es sich von jedem Zustand p in jeden anderen Zustand q überführen läßt.
Um die Steuerbarkeit zu prüfen, wurde von Kalman ein Kriterium entwickelt:
Der Rang der Matrix S = [B AB AAB ... A^n-1B] muß n sein.
Dabei ist B die Eingriffsmatrix, A die nxn Systemmatrix und B, AB, usw. sind insgesamt n Spalten der Matrix S. S ist auch eine nxn Matrix, wie A.
Rang einer Matrix
... Der Rang kann mit Hilfe des Gaußschen Eliminationsverfahrens bestimmt werden: Ergibt sich für eine nxn-Matrix ein Punkt bei einem beliebigen Zielvektor als Lösung, so ist der Rang maximal, nämlich n. Zeigen sich lineare Abhängigkeiten, so sinkt der Rang.
|
Da bei dem Kalman-Kriterium für eine nxn-Matrix der Rang n für S gefordert wird, kann einfach geprüft werden, ob die Determinante von S ungleich Null ist.
Untersuchung der Systemmatrizen aus der letzten Woche
Beispiel 1: A aus Code 0-26: "Entwurf und Simulation mit Zustandsregler für x und phi"
clear;
//Parameter:
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
//Auslegung des Zustandsreglers,
//der den Gesamtzustand ausregeln soll,
// also so, dass phi und x nach und
// nach zu Null werden, wobei phi
// schneller ausgeregelt werden soll.
A = [0 1 0 0
(m*g*h)/J 0 0 0
0 0 0 1
0 0 0 0];
B = [0; h/J; 0; 1/m];
//Steuerbarkeitsmatrix nach Kalman (vergl. Text weiter oben):
S = [B, A*B, A*A*B, A*A*A*B];
det(S) // ... liefert: 110813.87, also ungleich Null, also steuerbar.
Code 0-28: Bestimmung der Determinante der Steuerbarkeitsmatrix für den Zustandsregler mit 4x4-Matrix
Beispiel 2: I-Anteil ergänzt, wenn nur phi ausgeregelt wird
clear;
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
disp('Zustandsregler nur phi und omega und Integral phi');
// phi = d integ_phi/dt
A = [0 1 0
m*g*h/J 0 0
1 0 0];
B = [0; h/J; 0];
spec(A)
q=7.5594729;
EW = [-1, -q+q*%i, -q-q*%i];
R = ppol(A,B,EW)
A_stern = A-B*R
spec(A_stern)
S = [B,A*B,A*A*B]
det(S) // liefert -197.67060 ungleich Null!
Code 0-29: Untersuchung, wenn Integrativer Anteil ergänzt wird, aber nur phi ausgeregelt wird.
Beispiel 3: I-Anteil ergänzt, Integral von phi und x
clear;
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
disp('Zustandsregler nur phi, omega, x und v, Integral phi und Integral x');
A = [0 1 0 0 0 0
(m*g*h)/J 0 0 0 0 0
0 0 0 1 0 0
0 0 0 0 0 0
1 0 0 0 0 0
0 0 1 0 0 0 ];
B = [0; h/J; 0; 1/m; 0; 0];
spec(A)
q=7.5594729;
r=1.0;
EW = [-q+q*%i,-q-q*%i,-r-%i*r,-r+%i*r,-r,-r];
//R = ppol(A,B,EW) // auskommentiert, weil das Skript sonst abbricht.
//Astern = A - B*R;
//spec(Astern)
S = [B,A*B,A*A*B,A*A*A*B,A*A*A*A*B,A*A*A*A*A*B]
det(S) // ... liefert: 0 (Null!)
Code 0-30: ...ppol liefert hier: "Uncontrollable system", Die Determinante der Steuerungsmatrix det(S) liefert passend dazu Null!
Lösung des Problems
Die Struktur von B hatte sich aus den Systemgleichungen ergeben und repräsentiert, wie die Antriebskraft F auf das System einwirken kann: Dies geschieht einmal gemäß der Eulergleichung als Moment und zum zweiten gemäß der Newton-Gleichung in x-Richtung direkt als Kraft.
Für die neu eingeführten Zustände wurde der Einfluß bisher auf Null gesetzt. Jedoch spricht nichts dagegen ihn beispielsweise auf 1 zu setzen, da es sich hier ja um ergänzte Zustände handelt, mit denen "man machen kann, was immer man will":
clear;
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
disp('Zustandsregler nur phi, omega, x und v, Integral phi und Integral x');
A = [0 1 0 0 0 0
(m*g*h)/J 0 0 0 0 0
0 0 0 1 0 0
0 0 0 0 0 0
1 0 0 0 0 0
0 0 1 0 0 0 ];
//Idee: FA, aber auch phi und x sollen auf die I-Anteile zurückgeführt werden
//Vergl. Umsetzung in der Simulation weiter unten!
B = [0 0 0
h/J 0 0
0 0 0
1/m 0 0
1 1 1
1 1 1 ]; // NEU!!!!
spec(A)
q=7.5594729;
r=1.0;
EW = [-q+q*%i,-q-q*%i,-r-%i*r,-r+%i*r,-r,-r];
R = ppol(A,B,EW) // auskommentiert, weil das Skript sonst abbricht.
Astern = A - B*R;
spec(Astern)
S = [B,A*B,A*A*B,A*A*A*B,A*A*A*A*B,A*A*A*A*A*B];
rank(S) // ... liefert: 6
Code 0-31: ... liefert so erst einmal das gleiche Ergebnis (da ja die EW vorgegeben werden), wie ohne integrative Anteile. Ausstehend: Störverhalten und Verhaltenmit Totzeit im Vergleich.
Übung zum Invertierenden Pendel
Es soll der Einfluß von Totzeit und Störungen untersucht werden. Dies soll für die Variante, die nur phi ausregelt geschehen und im Anschluß auch für die, die auch nur phi ausregelt, aber einen integrativen Anteil ergänzt hat.
Vorgehen:
|
... MITTELWERT = 0.0; STREUUNG = 0.12; F_A = F_A + RAUSCHEN; ...
Code 0-32: Hilfestellung Gleichverteiltes Rauschen zu F_A
// Vergleich Zustandsregler ohne
// und mit integrativem Zustand
// Ausregelung von phi (nicht auch x)
clear;
disp('Teil 1: OHNE integrativem Anteil');
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
A = [0 1
m*g*h/J 0];
B = [0
h/J];
q = 7.5594729; //Betrag aus spec(A)
EW = [-q+%i*q;-q-%i*q];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B]
rank(S)
function ydot = rechteSeite(t,y)
phi=y(1,1);
omega=y(2,1);
F_A = -R*[phi;omega];
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
endfunction
t = 0:0.01:3;
y0 = [0.2;0.1];
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
clf;
plot(t,y(1,:),t,y(2,:));
disp('Teil 2: MIT integrativem Anteil');
A = [0 1 0
m*g*h/J 0 0
1 0 0];
B = [0
h/J
0];
q = 7.5594729; //Betrag aus spec(A)
//EW = [-q+%i*q;-q-%i*q;-q];
EW = [-q+%i*q;-q-%i*q;-1];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B, A*A*B]
rank(S)
function ydot = rechteSeiteInteg(t,y)
phi=y(1,1);
omega=y(2,1);
integ_phi=y(3,1);
F_A = -R*[phi;omega;integ_phi];
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
ydot(3,1) = phi;
endfunction
t = 0:0.01:3;
y0 = [0.2;0.1;0];
t0 = 0;
y = ode(y0,t0,t,rechteSeiteInteg);
plot(t,y(1,:),'blk--',t,y(2,:),'red--');
Code 0-33: vergleich1.sce
// Vergleich Zustandsregler ohne
// und mit integrativem Zustand
// Ausregelung von phi (nicht auch x)
// jetzt mit RuKu und Rauschen
clear;
MITTELWERT = 0.0;
STREUUNG = 0.5;
disp('Teil 1: OHNE integrativem Anteil');
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
A = [0 1
m*g*h/J 0];
B = [0
h/J];
q = 7.5594729; //Betrag aus spec(A)
EW = [-q+%i*q;-q-%i*q];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B]
rank(S)
function yneu=ruku(y,t,dt,modell)
k1=modell(t,y);
k2=modell(t+0.5*dt,y+0.5.*dt.*k1);
k3=modell(t+0.5*dt,y+0.5.*dt.*k2);
k4=modell(t+dt,y+dt.*k3);
yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6;
endfunction
function ydot = rechteSeite(t,y)
phi=y(1,1);
omega=y(2,1);
F_A = -R*[phi;omega];
RAUSCHEN = grand(1, 1, "nor", MITTELWERT, STREUUNG);
F_A = F_A + RAUSCHEN;
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
endfunction
y = [0.2;0.1];
tt= 0;
index=1;
dt = 0.01;
for t = 0:dt:3
yneu = ruku(y(1:2,index),t,dt,rechteSeite);
y = [y,yneu];
tt= [tt,t];
index=index+1;
end
clf;
plot(tt,y(1,:),tt,y(2,:));
disp('Teil 2: MIT integrativem Anteil');
A = [0 1 0
m*g*h/J 0 0
1 0 0];
B = [0
h/J
0];
q = 7.5594729; //Betrag aus spec(A)
EW = [-q+%i*q;-q-%i*q;-q];
//EW = [-q+%i*q;-q-%i*q;-1];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B, A*A*B]
rank(S)
function ydot = rechteSeiteInteg(t,y)
phi=y(1,1);
omega=y(2,1);
integ_phi=y(3,1);
F_A = -R*[phi;omega;integ_phi];
RAUSCHEN = grand(1, 1, "nor", MITTELWERT, STREUUNG);
F_A = F_A + RAUSCHEN;
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
ydot(3,1) = phi;
endfunction
y = [0.2;0.1;0];
tt= 0;
index=1;
dt = 0.01;
for t = 0:dt:3
yneu = ruku(y(1:3,index),t,dt,rechteSeiteInteg);
y = [y,yneu];
tt= [tt,t];
index=index+1;
end
plot(tt,y(1,:),'blk--',tt,y(2,:),'red--');
Code 0-34: vergleich2.sce
// Vergleich Zustandsregler ohne
// und mit integrativem Zustand
// Ausregelung von phi (nicht auch x)
// jetzt mit RuKu und Rauschen
clear;
dt=0.01;
Ttot = 0.1; // #### ANGEPASST ####
anztot = round(Ttot/dt)
xtotarr = zeros(anztot,1);
vtotarr = zeros(anztot,1);
MITTELWERT = 0.0;
STREUUNG = 0.5;
phitot=0;
omegatot=0;
disp('Teil 1: OHNE integrativem Anteil');
xtotarr = zeros(anztot,1);
vtotarr = zeros(anztot,1);
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
A = [0 1
m*g*h/J 0];
B = [0
h/J];
q = 7.5594729; //Betrag aus spec(A)
EW = [-q+%i*q;-q-%i*q];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B]
rank(S)
function yneu=ruku(y,t,dt,modell)
k1=modell(t,y);
k2=modell(t+0.5*dt,y+0.5.*dt.*k1);
k3=modell(t+0.5*dt,y+0.5.*dt.*k2);
k4=modell(t+dt,y+dt.*k3);
yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6;
endfunction
function ydot = rechteSeite(t,y)
phi=y(1,1);
omega=y(2,1);
F_A = -R*[phitot;omegatot];
RAUSCHEN = grand(1, 1, "nor", MITTELWERT, STREUUNG);
F_A = F_A + RAUSCHEN;
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
endfunction
y = [0.2;0.1];
tt= 0;
index=1;
dt = 0.01;
for t = 0:dt:3
yneu = ruku(y(1:2,index),t,dt,rechteSeite);
y = [y,yneu];
tt= [tt,t];
phitot = xtotarr(modulo((index-1),anztot)+1);
xtotarr(modulo((index-1),anztot)+1)=yneu(1);
omegatot = vtotarr(modulo((index-1),anztot)+1);
vtotarr(modulo((index-1),anztot)+1)=yneu(2);
index=index+1;
end
clf;
plot(tt,y(1,:),tt,y(2,:));
disp('Teil 2: MIT integrativem Anteil');
xtotarr = zeros(anztot,1);
vtotarr = zeros(anztot,1);
phitot=0;
omegatot=0;
A = [0 1 0
m*g*h/J 0 0
1 0 0];
B = [0
h/J
0];
q = 7.5594729; //Betrag aus spec(A)
EW = [-q+%i*q;-q-%i*q;-q];
//EW = [-q+%i*q;-q-%i*q;-1];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B, A*A*B]
rank(S)
function ydot = rechteSeiteInteg(t,y)
phi=y(1,1);
omega=y(2,1);
integ_phi=y(3,1);
F_A = -R*[phitot;omegatot;integ_phi];
RAUSCHEN = grand(1, 1, "nor", MITTELWERT, STREUUNG);
F_A = F_A + RAUSCHEN;
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
ydot(3,1) = phi;
endfunction
y = [0.2;0.1;0];
tt= 0;
index=1;
dt = 0.01;
for t = 0:dt:3
yneu = ruku(y(1:3,index),t,dt,rechteSeiteInteg);
y = [y,yneu];
tt= [tt,t];
phitot = xtotarr(modulo((index-1),anztot)+1);
xtotarr(modulo((index-1),anztot)+1)=yneu(1);
omegatot = vtotarr(modulo((index-1),anztot)+1);
vtotarr(modulo((index-1),anztot)+1)=yneu(2);
index=index+1;
end
plot(tt,y(1,:),'blk--',tt,y(2,:),'red--');
Code 0-35: vergleich3.sce
Dienstag 21.06.2021
Themen
|
Übung 1
Gegeben seien die Systemmatrix A und die Eingriffsmatrix B einer Regelstrecke:
$ A=\left[\begin{array}{cc}0 & 1 \\ -4 & 0\end{array}\right] $
Formel 0-14: Systemmatrix A
$ B=\left[\begin{array}{cc}0 \\ 2\end{array}\right] $
Formel 0-15: Eingriffsmatrix B
|
Hinweis: Führen Sie die Aufgabenteile zunächst immer alle von Hand aus, aber überprüfen die Richtigkeit danach mit Hilfe von Scilab.
Gehen Sie für die nachfolgenden Paare von A und B genauso vor:
Übung 1 Teil b)
$ A=\left[\begin{array}{cc}0 & 1 \\ 4 & 0\end{array}\right] $
Formel 0-16: Systemmatrix A
$ B=\left[\begin{array}{cc}0 \\ 1\end{array}\right] $
Formel 0-17: Eingriffsmatrix B
Übung 1 Teil c)
$ A=\left[\begin{array}{cc}0 & 1 \\ -1 & 0\end{array}\right] $
Formel 0-18: Systemmatrix A
$ B=\left[\begin{array}{cc}1 \\ 1\end{array}\right] $
Formel 0-19: Eingriffsmatrix B
Übung 1 Teil d)
$ A=\left[\begin{array}{cc}0 & 1 \\ 0 & 1\end{array}\right] $
Formel 0-20: Systemmatrix A
$ B=\left[\begin{array}{cc}0 \\ 1\end{array}\right] $
Formel 0-21: Eingriffsmatrix B
Übung 1 Teil e)
$ A=\left[\begin{array}{cc}0 & 1 \\ -1 & -1\end{array}\right] $
Formel 0-22: Systemmatrix A
$ B=\left[\begin{array}{cc}0 \\ 1\end{array}\right] $
Formel 0-23: Eingriffsmatrix B
Übung 2
|
Hinweis: Führen Sie wieder die Aufgabenteile zunächst immer alle von Hand aus, aber überprüfen die Richtigkeit danach mit Hilfe von Scilab.
Quiz
|
Nachtrag zu I-Anteil in Zustandsreglern
In einem Simulationsversuch wurden kummulativ gleich mehrere negative Einflußgrößen auf das zu regelnde System angewendet:
|
Insbesondere 3. liefert Aussagen über die Robustheit eines Reglers: Arbeitet er auch noch bei Meß- bzw. Modellungenauigkeiten zufriedenstellend?
Der zusätzliche Kraftstoß wurde aufgrund folgender Überlegung (und vorangegangener vergeblicher Versuche, die Überlegenheit einer Anordnung mit I-Anteil zu zeigen) eingeführt: Der I-Anteil besitzt zu Beginn der Simulation völlig falsche Werte. Erst nach dem Einschwingen kann er somit sinnvoll zur Geltung kommen.
Erst durch Einführen des Kraftstoßes lassen sich deutliche Verbesserungen am Verhalten des geregelten Systems bei Einführung eines I-Anteils als "virtuellen" zusätzlichen Zustand erkennen:
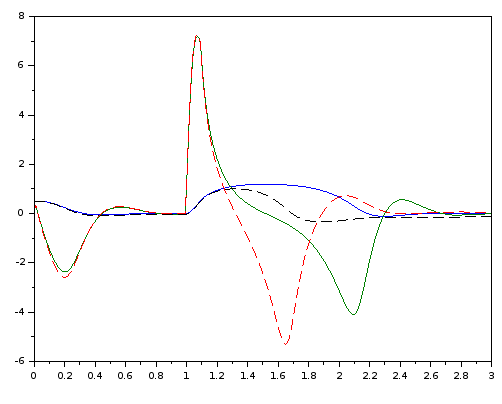
Bild 0-7: Kraftstoß von 33N ab t=1s für 0,1s: Das System mit I-Anteil (gestrichelt) regelt deutlich schneller aus.
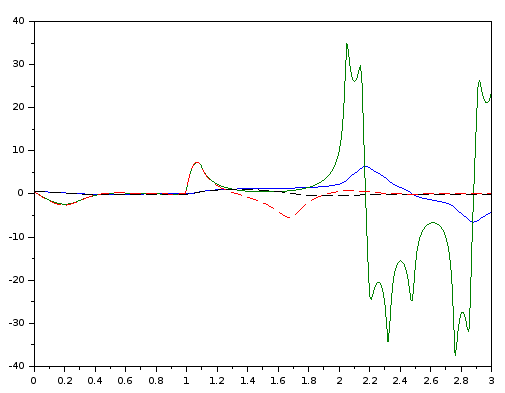
Bild 0-8: Kraftstoß von 33,5N ab t=1s für 0,1s: Das System ohne I-Anteil (durchgezogen) wird instabil.
Den Simulationsexperimenten lag folgendes Scilab-Skript zugrunde:
// Vergleich Zustandsregler ohne
// und mit integrativem Zustand
// Ausregelung von phi (nicht auch x)
// jetzt mit RuKu und Rauschen
clear;
dt=0.01;
Ttot = 0.01; // #### ANGEPASST ####
anztot = round(Ttot/dt)
xtotarr = zeros(anztot,1);
vtotarr = zeros(anztot,1);
MITTELWERT = 0.0;
STREUUNG = 0.1;
FSTOER = 33.0; //effekt1
//FSTOER = 33.5; //effekt2
MFEHLER = 1.2;
phitot=0;
omegatot=0;
disp('Teil 1: OHNE integrativem Anteil');
xtotarr = zeros(anztot,1);
vtotarr = zeros(anztot,1);
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
A = [0 1
m*g*h/J 0];
B = [0
h/J];
q = 7.5594729; //Betrag aus spec(A)
EW = [-q+%i*q;-q-%i*q];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B]
rank(S)
function yneu=ruku(y,t,dt,modell)
k1=modell(t,y);
k2=modell(t+0.5*dt,y+0.5.*dt.*k1);
k3=modell(t+0.5*dt,y+0.5.*dt.*k2);
k4=modell(t+dt,y+dt.*k3);
yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6;
endfunction
m = MFEHLER;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
function ydot = rechteSeite(t,y)
phi=y(1,1);
omega=y(2,1);
F_A = -R*[phitot;omegatot];
RAUSCHEN = grand(1, 1, "nor", MITTELWERT, STREUUNG);
F_stoer=0;
if t>1 && t<1.1 then
F_stoer=FSTOER;
end;
F_A = F_A + RAUSCHEN+F_stoer;
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
endfunction
y = [0.5;0.0];
tt= 0;
index=1;
dt = 0.01;
for t = 0:dt:3
yneu = ruku(y(1:2,index),t,dt,rechteSeite);
y = [y,yneu];
tt= [tt,t];
phitot = xtotarr(modulo((index-1),anztot)+1);
xtotarr(modulo((index-1),anztot)+1)=yneu(1);
omegatot = vtotarr(modulo((index-1),anztot)+1);
vtotarr(modulo((index-1),anztot)+1)=yneu(2);
index=index+1;
end
clf;
plot(tt,y(1,:),tt,y(2,:));
disp('Teil 2: MIT integrativem Anteil');
m = 1.0;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
xtotarr = zeros(anztot,1);
vtotarr = zeros(anztot,1);
itotarr = zeros(anztot,1);
iphitot=0;
phitot=0;
omegatot=0;
A = [0 1 0
m*g*h/J 0 0
1 0 0];
B = [0
h/J
0];
q = 7.5594729; //Betrag aus spec(A)
EW = [-q+%i*q;-q-%i*q;-0.05*q];
//EW = [-q+%i*q;-q-%i*q;-1];
R = ppol(A,B,EW);
A_stern = A-B*R
spec(A_stern)
S = [B, A*B]
rank(S)
m = MFEHLER;
l = 1.0;
h = 0.5;
r = 0.1;
g = 9.81;
J = 1/4 * m* r*r + 1/12 * m * l*l;
function ydot = rechteSeiteInteg(t,y)
phi=y(1,1);
omega=y(2,1);
integ_phi=y(3,1);
F_A = -R*[phitot;omegatot;iphitot];
RAUSCHEN = grand(1, 1, "nor", MITTELWERT, STREUUNG);
F_stoer=0;
if t>1 && t<1.1 then
F_stoer=FSTOER;
end;
F_A = F_A + RAUSCHEN+F_stoer;
ydot(1,1) = omega;
ydot(2,1) =(m*g*h*sin(phi)-m*h*h*omega*omega*cos(phi)*sin(phi)+F_A*h*cos(phi))/(J+m*h*h*sin(phi)*sin(phi));
ydot(3,1) = phi;
endfunction
y = [0.5;0.0;0.0];
tt= 0;
index=1;
dt = 0.01;
for t = 0:dt:3
yneu = ruku(y(1:3,index),t,dt,rechteSeiteInteg);
y = [y,yneu];
tt= [tt,t];
phitot = xtotarr(modulo((index-1),anztot)+1);
xtotarr(modulo((index-1),anztot)+1)=yneu(1);
omegatot = vtotarr(modulo((index-1),anztot)+1);
vtotarr(modulo((index-1),anztot)+1)=yneu(2);
iphitot = itotarr(modulo((index-1),anztot)+1);
itotarr(modulo((index-1),anztot)+1)=yneu(3);
index=index+1;
end
plot(tt,y(1,:),'blk--',tt,y(2,:),'red--');
Code 0-36: Scilab-Skript zur Untersuchung der Unterschiede zwischen einem Zustandsregler mit virtuellem integrativen Zustand und ohne.