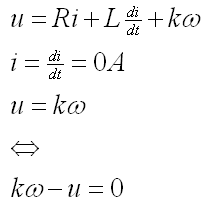Übung7: Parameteridentifikation mit Hilfe der Methode der kleinsten Quadrate
Aufgabe 1
- Ein stehender Gleichstrom-Motor bringt bei verschiedenen Versorgungsspannungen über einen Hebelarm unterschiedliche Momente auf eine Waage auf.
- Rechnen Sie die Meßtabelle U, I, Gewicht (muß in Moment umgerechnet werden) passend für die Modellgleichungen um unbestimmen Sie mit LSQ die Modellparameter km und H
|
zu Aufgabe 1: Die Messungen
- Die Modellgleichungen bilden die Systemstruktur ab.
- Die Modellgleichungen, Modellparameter und Anfangsbedingungen bestimmen gemeinsam das Systemverhalten.
- Die Modellparameter müssen am realen System gemessen werden.
- In der Regel sind sie fehlerbehaftet.
- Häufig gibt es gar keine Möglichkeit die Parameter zu messen und man muß sie aus theoretischen Überlegungen heraus abschätzen.
- Die Methode der kleinsten Quadrate bietet die Möglichkeit, aus einer Vielzahl an Messungen die Modellparameter so
zu bestimmen, dass das Quadrat der Fehler zwischen Modell und System minimiert wird.
- Lineare Regression ist ein Spezialfall der Methode der kleinsten Quadrate. Um das
Arbeitsprinzip zu verstehen wird zunächst die Lineare Regression theoretisch hergeleitet.
|
Mechanische Parameter
- Hebelmaterial: 2mm Kupferdraht
- Hebelgewicht: 0,8gramm
- Hebellänge: 45,6mm
|
Versuch
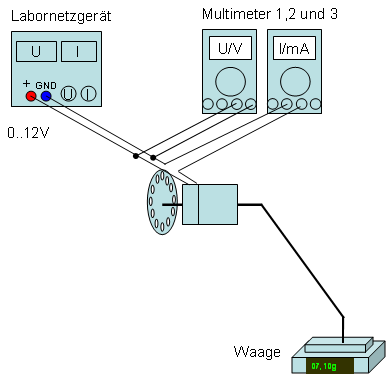
Bild 0-1: Statisches Moment in abhängigkeit der elektrischen Eingangsleistung.
U/V I/mA Gewicht/gramm
2.0 106.5 3.6
3.0 157.8 5.4
4.0 206.4 7.1
5.0 253.0 8.9
6.0 293.4 10.5
7.0 315.0 11.6
8.0 390.0 14.6
9.0 410.0 15.1
10.0 440.0 16.7
11.0 460.0 17.6
12.0 480.0 17.9
Code 0-1: Auf der Waage aufgebrachtes Gewicht in Abhängigkeit der elektrische Eingangsleistung des Motors.
zu Aufgabe 1: Die Modellgleichung
- In diesem Versuch wurde die auf eine Waage durch den Motor über einen Hebelarm aufgebrachte Kraft gemessen und der Motorstrom.
- Zusammen mit der mechanischen Modellgleichung und ω=0rad/s kann man daraus km bestimmen:
|

Bild 0-3: Reduzierte mechanische Modellgleichung, Umformung für LSQ.
- Wir betrachten hier das abgegebene Moment M.
- Es wird reduziert um die Haftreibung.
- Unbekannte sind für LSQ die Parameter km und H.
|
Bestimmen Sie aufgrund der obigen Angaben km und H
mit Hilfe der Methode der kleinsten Quadrate.
Aufgabe 2 - Bestimmung der Generator-Konstanten unter Ausnutzung des Dynamoeffekts
- In dem Versuch wurde ein baugleicher Motor als Dynamo an den andern angekoppelt.
- So konnte die induzierte Spannung e in Abhängigkeit der Winkelgeschwindigkeit ω gemessen werden.
- Aus dieser Reihe und der reduzierten elektrischen Modellgleichung kann über LSQ k bestimmt werden.
- Reduktion der Modellgleichung:
|
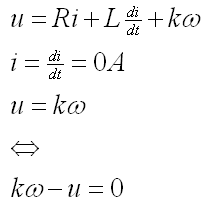
Bild 0-1: Reduzierte Modellgleichung, Umformung für LSQ.
zu Aufgabe 2: Der Versuch
- Anordnung wie zuvor, aber an den Motor wird ein zweiter über eine Kupplung verbunden.
- Die induzierte Spannung (Dynamo-Effekt) wird in Abhängigkeit der Frequenz, die die Lochscheibe liefert aufgezeichnet.
- Die Lochscheibe hat zwölf Bohrungen, liefert pro Umdrehung also zwölf Pulse.
|
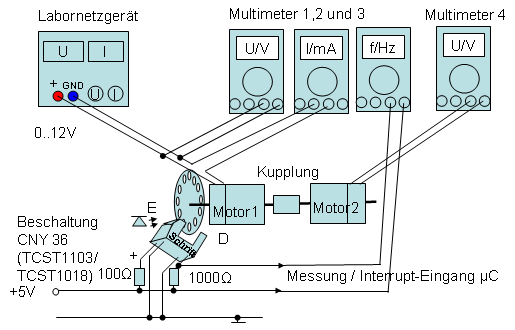
Bild 0-1: Versuchsanordnung für Induzierte Spannung e.

Bild 0-2: Versuchsanordnung für Induzierte Spannung e - gekoppelte Motoren.
f/Hz e/V
80.0 0.67
186.0 1.61
281.0 2.45
371.0 3.22
462.0 4.06
578.0 5.00
696.0 6.00
824.0 7.10
938.0 8.07
1047.0 9.03
1148.0 9.97
Code 0-1: Induzierte Spannung e/V in Abhängigkeit der Lochscheibenfrequenz f/Hz

Bild 0-1: Diagramm zur induzierten Ankerspannung e.
Bestimmen Sie aufgrund der obigen Angaben k
mit Hilfe der Methode der kleinsten Quadrate.