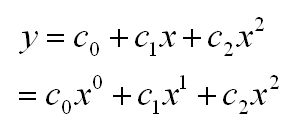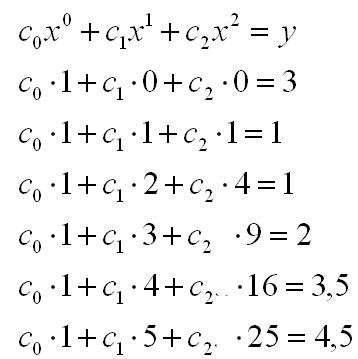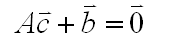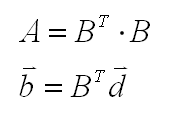Darstellen des Verfahrens anhand eines exemplarischen Beispiels
Das Problem
- Es wird angenommen, dass der Zusammenhang zwischen der Größe x und der
Größe y durch folgende empirische Formel gut beschrieben werden kann:
|
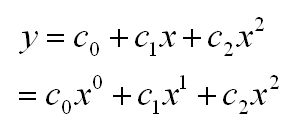
Bild 0-1: Empirische Formel.
- Messungen lieferten folgende Wertepaare zu x und y:
|
| x |
0.0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
| y |
3.0 |
1.0 |
1.0 |
2.0 |
3.5 |
4.5 |
Tabelle 0-1: Messreihe
Wie wird aus Messungen und Formel das überbestimmte Gleichungssystem gemacht?
- Jedes Messwertpaar und die Gleichung liefert eine
Bestimmungsgleichung für c0,c1 und c2:
|
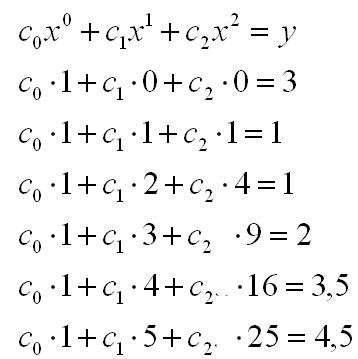
Bild 0-2: Bestimmungsgleichungen für c0,c1,c2.
- Hier wird deutlich, dass x und y festliegen und c0,c1,c2 die variablen Größen sind.
- Ferner widersprechen sich die Gleichungen ganz offenbar. D.h. sie sind alle
mit einem Fehler r (für Residuum) behaftet:
- Die vorhergehenden Gleichungen in Matrixschreibweise
mit den Fehlern r kann dann so geschrieben werden:
- Bei der kleinsten Quadrate-Methode wird gerade dafür
gesorgt, dass die Summe der Quadrate der Fehler r minimiert
werden.
|

Bild 0-3: Bestimmungsgleichungen in Matrixschreibweise
Vorgehen bei der Methode der kleinsten Quadrate
- Bei der Methode der kleinsten Quadrate
muss folgendes lineares Gleichungssystem gelöst werden:
|
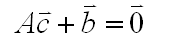
Bild 0-4: Zu lösendes LGS bei kleinster Quadrate Methode.
- c entspticht dabei dem gesuchten Vektor mit c0,c1,c2
- Die anderen Größen A und b werden aus B und d folgendermaßen gebildet:
|
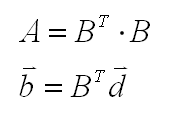
Bild 0-5: Formeln zur Bildung von A und b.
- Für das Beispiel ergibt sich dann A und b folgendermassen:
|

Bild 0-5: Bildung von A und b.
- Zur Lösung des Gleichungssystems Ac+b=0 werden Sie wenn Sie es von Hand durchführen
sinnvollerweise den Gauss-Algorithmus verwenden.
- Typischerweise wird aber die Cholesky-Zerlegung
bei Implementationen verwendet, weil diese ca. halb so viele
Rechenoperationen erfordert und die Voraussetzungen für
deren Anwendung bei dem LGS Ac+b=0 immer erfüllt sind (z.B. A positiv definit).
|
- Im folgenden sollen beide Lösungsverfahren gezeigt werden.
|