Integration mit Hilfe von Scilab
1:1 Umsetzung des C++ Programms in Scilab
- Scilab ist ein Open-Source-Programm mit ähnlicher Syntax und Funktionalität wie das kommerzielle Programm für wissenschaftliches Rechnen Matlab
- Ein ähnliches Programm, auch Open-Source wäre noch Octave
- Nach Start->scilab-4.0->scilab-4.0 erscheint eine Konsole, in der direkt eingegebene Befehle ausgeführt werden:
- Enden sie mit einem Semikolon, so wird das Ergebnis einer Operation nicht angezeigt.
- Die Stärke von Scilab/Octave/Matlab liegt in der schnellen Verarbeitung von Matrizen und einer riesigen Bibliothek an mathematischen Funktionen und zur Ergebnisdarstellung.
- Schleifen laufen dagegen eher langsam ab.
- ACHTUNG: Im Gegensatz zu C,C++, oder Java, beginnen hier die Indizes von Arrays mit 1 und nicht mit 0.
- Mit eckigen Klammern angelegte Vektoren liegen.
- Mit einem nachfolgenden Hochkomma werden sie transponiert.
|

Bild 0-1: Beispielbefehle in Scilab
- Statt einzelner Befehle, kann auch ein Skript in einem File mit Endung .m zusammengestellt werden.
- Im folgenden ist das vorhergehende C++ - Programm fast 1:1 als Scilab-Makro umgesetzt.
- Es wird z.B. in Notepad geschrieben und unter einem Namen mit .sce oder .m - Endung abgespeichert.
- Im Scilab-Fenster kann man dann in das entsprechende Verzeichnis mit cd DATEIPFAD gehen und das Makro hier mit exec euler.m starten.
- Die Angaben 1:ii-1 sind übrigens nötig, weil etwas mehr Speicher von Scicos automatisch allokiert wird, als nötig.
|
A=20
dt=60
k=1/872542
sekunden_pro_tag = 86400
tage = 30
schritte = (tage*sekunden_pro_tag)/dt
schritte_pro_tag = round(sekunden_pro_tag/dt)
t=0
ii=1
for i=0:1:schritte
if(modulo(i,schritte_pro_tag)==0)
merke_t(ii) = t;
merke_A(ii) = A;
ii=ii+1;
end
t=t+dt;
A = A*(k*dt + 1);
end
plot(merke_t(1:ii-1),merke_A(1:ii-1),'*blu-');
//siehe help axes_properties
a = gca();
a.x_label.text = 't/s';
a.y_label.text = 'A/m2';
a.title.text = 'Flächenwachstum eines Seerosenteiches';
Code 0-1: Scilab-Makro euler.m zur Euler-Integration des Seerosenteich-Modells

Bild 0-2: Beispiel in Scilab etwas übersichtlicher ohne Grafik.
 seerose_scilab.zip, enthält euler.m
seerose_scilab.zip, enthält euler.m
Wie man sieht, kommt man hier sehr leicht an eine ansprechende Visualisierung der Ergebnisse.
Die folgende Scilab-plot-Grafik wurde mit dem Befehl File->export als gif-Bild exportiert.
Leider gibt es bei der Y-Achsen-Beschriftung beim Exportieren ein Problem.
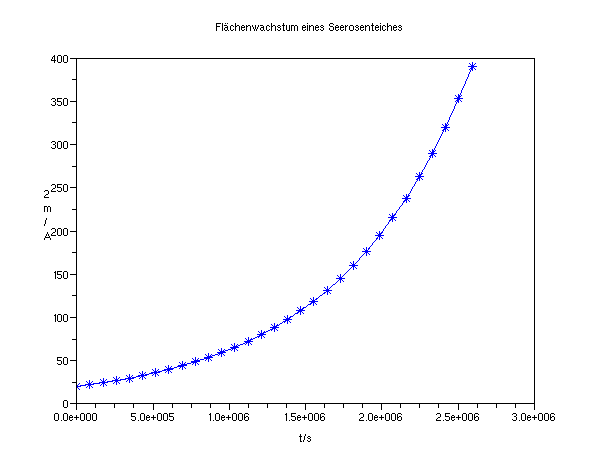
Bild 0-2: Ergebnis der Scilab-Berechnung mit plot(merke_t(1:ii-1),merke_A(1:ii-1),'*blu-'); dargestellt.
Vergleich mit dem analytischen Ergebnis
- Nach Ablauf des Makros werden nun noch die folgenden Zeilen eingegeben, um auch die analytische Berechnung durchzuführen:
|
Aneu = 20*exp(merke_t(1:ii-1)/872542);
plot(merke_t(1:ii-1),merke_A(1:ii-1),merke_t(1:ii-1),Aneu);
Code 0-2: Vergleich zwischen analytischer und numerischer Berechnung
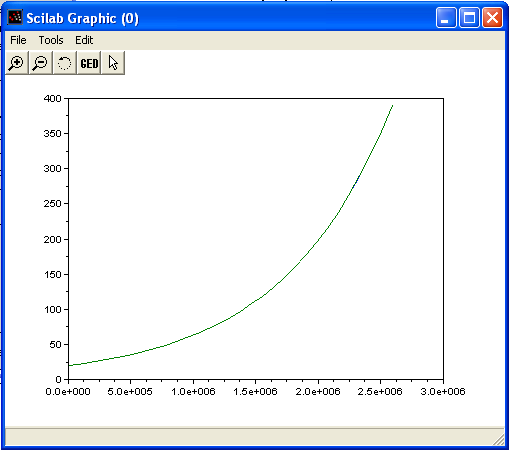
Bild 0-3: Übereinander liegende analytische und numerische Ergebniskurve.
- Die Beiden Kurven liegen augenscheinlich weitgehend deckungsgleich übereinander. Mehr Informationen
bringt die Darstellung der absoluten Differenz beider Ergebnis, also quasi der absolute
Fehler der numerischen Integration:
- Folgende Befehle liefern die gewünschte Kurve:
|
Fehler = abs( merke_A(1:ii-1) - Aneu );
plot(merke_t(1:ii-1),Fehler);
Code 0-3: Absolute Differenz zwischen analytischer und numerischer Berechnung
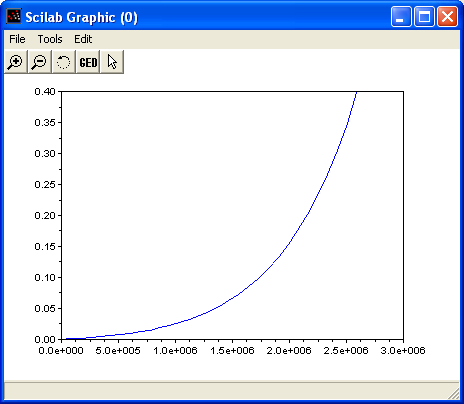
Bild 0-4: Verlauf des absoluten Fehlers der numerischen Integration.
Hier wird schon deutlich, dass sich der numerische Fehler bei der numerischen Integration
mit dem Euler-Verfahren Schritt für Schritt aufsummiert und somit exponentiell anwächst.


 seerose_scilab.zip, enthält euler.m
seerose_scilab.zip, enthält euler.m


