Berechnung des Flächenwachstums der Seerosen mit dem Eulerschen Integrationsverfahren
Hinter A in unserer Differentialgleichung steht eine uns unbekannte Funktion A(t), die die Seerosenfläche zu jedem Zeitpunkt angibt.
Würden wir A(t) kennen, dann hätten wir eine so genannte geschlossene Lösung des Problems und damit die Lösung der Differentialgleichung.
Wir werden noch sehen, wie man an die geschlossene Lösung in diesem Fall kommt. In vielen anderen Fällen läßt sich eine solche geschlossene Lösung nicht berechnen und man greift auf das Mittel der numerischen Integration zurück, um den Zustand des Modells zu jedem Zeitpunkt zu berechnen.
Das wohl einfachste (aber auch ungenaueste) Verfahren zur numerischen Behandlung von Differentialgleichungen stellt das Eulersche Integrationsverfahren dar.
Was dieses ist, soll anhand des Seerosenbeispiels hier praktisch gezeigt werden:
Wir gehen wieder von unserer Seerosen-Modellgleichung aus:
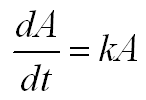
Bild 0-1: Modellgleichung für das Flächenwachstum der Seerosen auf dem Teich.
Zur Vorbereitung der numerischen Integration ersetzen wir das Differential durch den Differenzenquotienten:
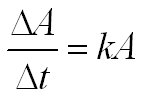
Bild 0-2: Modellgleichung für das Flächenwachstum der Seerosen auf dem Teich mit Differenzenquotienten.
Anschaulich heisst das:
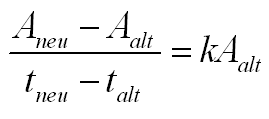
Bild 0-3: Modellgleichung für das Flächenwachstum der Seerosen auf dem Teich mit Differenzenquotienten anschaulicher.
|
Wir führen zuvor noch äquidistante, diskrete Zeitschritte t0,t1,t2,...ti,ti+1,...tn ein und die immer gleiche Differenz zwischen zwei Zeitschritten Δt.
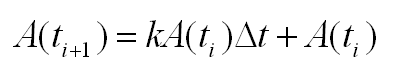
Bild 0-4: Modell-Differenzengleichung nach neuer Fläche aufgelöst.
Kennen wir nun den Faktor k und die Fläche zu einem Startzeitpunkt t0, also A(t0), oder kurz A0, so können wir nun durch wiederholtes Anwenden der obigen Formel A1, A2, A3, usw. bestimmen, wobei immer das Ergebnis der Berechnung von Ai vorliegen muss, um Ai+1 bestimmen zu können.
A0 nennen wir dann Anfangsbedingung der Integration.
Das, was wir dann tuen, ist die Durchführung einer numerischen Integration mit Hilfe des Eulerschen Integrationsverfahrens. Wir erinnern uns: Integrieren heisst das Aufsummieren von Steigungen zwischen einem Startpunkt und einem Zielpunkt:
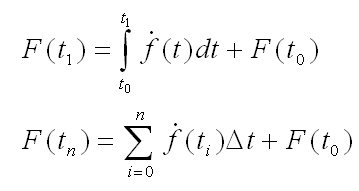
Bild 0-5: Bestimmtes Integral: Vergleich mit Differential und Differenz für t. ACHTUNG: t1 im oberen kontinuierlichen Fall entspricht tn in der diskreten unteren Gleichung.