Lineare Regression

Trägt man die Messungen in einem Koordinatensystem als Punkte ein, so erhält man im allgemeinen Fall einePunktwolke.

Lägen alle Punkte auf einer Geraden, dann hätte man keine Messfehler und der Zusammenhang zwischen denWertepaaren wäre linear.

Wenn aber im allgemeinen Messfehler vorliegen, dann stellt sich die Frage, wie man eine Gerade amso durch die Punkte hindurchlegen kann, dass sie im Durchschnitt überall möglichst nah an den Messpunkten liegt.

Eine mögliche Lösung dieses Problems stellt die lineare Regression dar.

Sind die Messpunkte Wertepaare (x1,y1), (x2,y2), (x3,y3)...(xn,yn), so trifft die passende Geradengleichungy=bx+a in der Regel nicht genau auf die Punkte, sondern es gibt bei jedem Wertepaar einen mehr oderweniger grossen Fehler ei:

y1=bx1+a+e1
y2=bx2+a+e2
y3=bx3+a+e3
...
yn=bxn+a+en

Mit Hilfe der Formel für die lineare Regression können nun a und b so bestimmt werden,dass die Summe der quadrierten Fehler minimal wird, also e₁² + e₂² + e₃² + ... + e_n²möglichst klein wird.

Hier zunächst die Formeln zur optimalen Bestimmung von a und b aus allen Messwerten:

Nun wäre es natürlich noch interessant zu erfahren, wie man auf die Formel für die Lineare Regression kommt.

Hier ist die Herleitung dazu:

Die Summe des quadrierten Fehlers läßt sich folgendermassen schreiben (vergl. weiter oben):

Diesen Fehler gilt es zu minimieren.Ein notwendiges Kriterium dafür, dass eine Funktion ein lokales Extremum erreicht, ist, dass ihreerste Ableitung zu Null wird.

Achtung: Hier geht es um die Festlegung von a und b! a und b sind hier die Variablen, die anderen Größensind bei konkreten Messwerten alle konstant. Darum wird die Gleichung für die Summe der Fehlerquadratejeweils nach a und nach b abgeleitet und von beiden Ergebnissen verlangt, dass sie zu Null werden.

Da die Gleichung sowohl von a als auch von b abhängt, und bei den Ableitungen die jeweils nicht betrachtete Größe als konstant angesehen wird, spricht man hier von einer partiellen Ableitung nach a und b. Hierfür werden gerundete Differentialsymbole geschrieben. Ansonsten gelten die üblichen Ableitungsregeln, hier wird insbesondere dadurch abgeleitet, dass man die äußere Ableitung der Klammermit der inneren multipliziert:

Das folgende sind zunächst Äquivalenzumformungen von A1 und B1:

Nun wird A2 durch n geteilt und mit 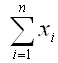multipliziert und zu Gleichung B2 addiert.Man erhält dann:

Diese kann nach b aufgelöst werden:

Parameter a ergibt sich dann aus Gleichung A2 durch einsetzen des nun bekannten Parameters b: