Lösungen zu Übung 10 - Prozedurales Programm in objektorientierte Form bringen
Hinweise zu dieser Lehrveranstaltung
- Nicht alle Lehrinhalte werden im Internet veröffentlicht.
- Bitte besorgen Sie sich die Mitschrieb von Ihren Mitstudierenden, wenn Sie eine Vorlesung verpaßt haben und holen den Stoff nach.
- Es ist günstig, einen Ordner mit dem Ausdruck dieser Vorlesung anzulegen und mit schriftlichen Ergänzungen zu vervollständigen.
|
Erste Lösungsidee zur objektorientierten Umsetzung des Simulationsprogramms:
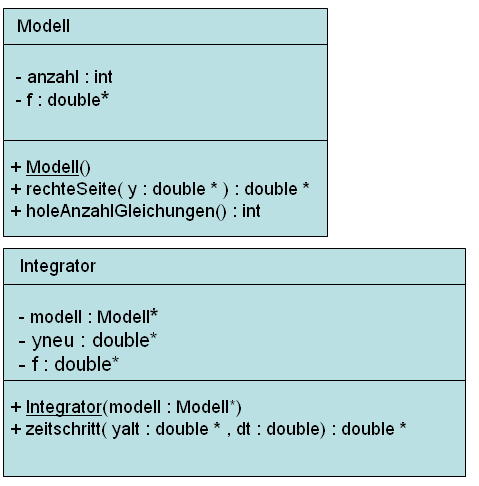
Bild 0-1: Entwurf eines ersten Simulationsprogrammes mittels UML-Klassendiagramm.
- Die Klasse "Modell" repräsentiert das Simulationsmodell.
- Die hier verwendeten Modelle werden durch Differentialgleichungssysteme erster Ordnung beschrieben.
- Die Funktion "rechteSeite()" liefert die Steigung an der mit y übergebenen Stelle.
- y enthält bei ist bei unserem ersten Modell ein Array mit zwei Werten, in dem der aktuelle Wert für die Auslenkung x und die Geschwindigkeit v des Schwingers gespeichert ist.
- Die Funktion "rechteSeite()" liefert also als erste Komponente die Steigung von x und als zweite die Steigung von v.
- Da andere Modelle aus mehr Gleichungen, oder nur einer bestehen könnten, wird in der Variable "anzahl" die Anzahl der Modellgleichungen für das aktuelle Modell gespeichert.
|
- Die Integrator-KLasse enthält die Funktion "...zeitschritt(...)", die aus einem übergebenen Zustand zum Zeitpunkt t den Nachfolgezustand zum Zeitpunkt t+Δt berechnet.
- Bei der Eulerintegration geschieht dies durch Hinzuzählen der mit Δt multiplizierten aktuellen Steigung zum aktuellen Zustand.
- Da es mehrere Zustandsgrößen (hier zwei: x und v) gibt, für die diese Prozedur ausgeführt werden muß, benötigt der Integrator eine Information darüber, wieviele Zustände pro Zeitschritt integriert werden müssen.
- Diese Information liefert das Modell durch die Funktion "..holeAnzahlGleichungen()", welche den Wert des Objektattributs "anzahl" zurückgibt.
- Damit der Integrator "weiß", welches Modell er integrieren muß und auch Zugriff darauf hat, gibt es in der Integrator-Klasse ein Objektattribut vom Typ Modell*.
- In dieser Variable wird ein Zeiger auf das zu integrierende Modell abgelegt.
- Der Zeiger wird mit Hilfe des Konstruktors der Integrator-Klasse mit demjenigen Modell belegt, dessen Zeiger dem Konstruktor als Übergabeparameter übergeben wird.
|
- Auf diese Weise sind nun das Integrationsverfahren und die Modellgleichungen voneinander getrennt worden und es wurden zwei KLassen entwickelt, die diese Elemente in Form von Funktionen beinhalten.
- Die UML-Diagramme sind eher C++ orientiert.
- Umsetzung und Weiterentwicklung in Java: s. Vorlesung.
|
sim.zip - in Vorlesung zu entwickelnde Programme.
Übung 10
- Grundlage bildet das in der Vorlesung entwickelte objektorientierte Simulationsprogramm, das Sie weiter oben unter sim.zip herunterladen können.
- Schreiben Sie ergänzend zu diesem Programm eine Klasse RuKuIntegrator, der den vorher dargestellten Runge-Kutta-Integrations-Algorithmus implementiert.
- Gehen Sie dabei genauso vor, wie bei der in der Vorlesung entwickelten Klasse EulerIntegrator.
- Verwenden Sie insbesondere auch für Ihre Klasse die Oberklasse Integrator.
- Tauschen Sie die Euler-Integrationsklasse durch Ihre Integrator-Klasse aus.
- Nutzen Sie diese Aufgabe, um noch einmal das bisher entwickelte Simulationsprogramm zu analysieren.
|