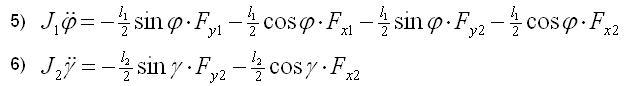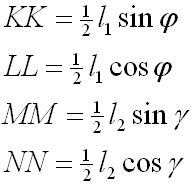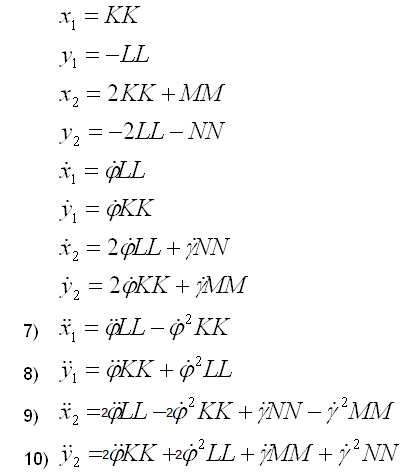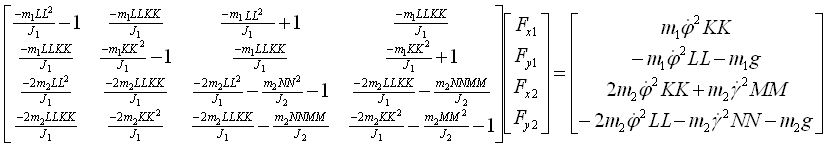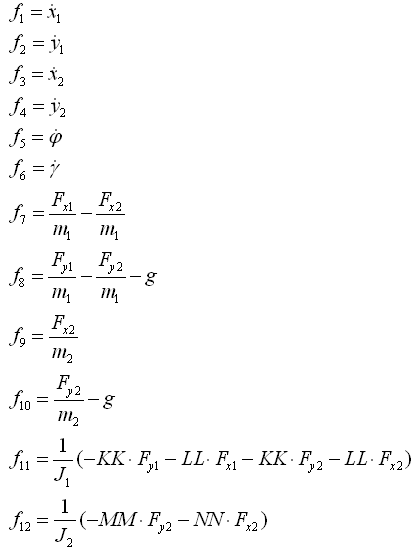Herleitung für die Simulationsgleichungen eines Doppelpendels
(EN google-translate)
(PL google-translate)
 doppelpendel_vrml.zip - Entwicklung einer Musterlösung für die Animation des Doppelpendels.
doppelpendel_vrml.zip - Entwicklung einer Musterlösung für die Animation des Doppelpendels.
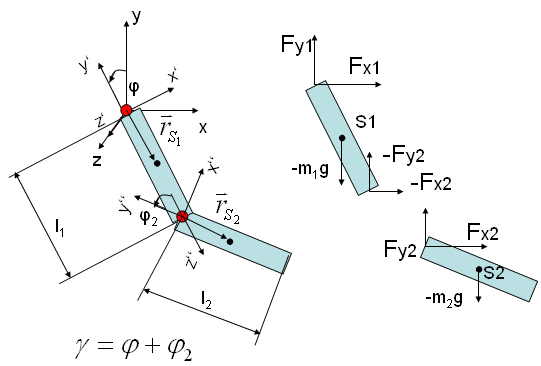
Bild 0-1: Doppelpendel mit Schnittkräften
Aufstellen der Newton-Eulerschen Gleichungen
- Alle Formeln werden bzgl. des Inertialkoordinatensystems aufgestellt.
- Kräfte und Momente in den Eulergleichungen werden bzgl. des Schwerpunktes des jeweiligen Körpers aufgestellt.
|

Bild 0-2: Die sechs Newton-Eulerschen Gleichungen des Doppelpendels
- Die Kreuzprodukte für die Momente in den Eulergleichungen führen zu:
|
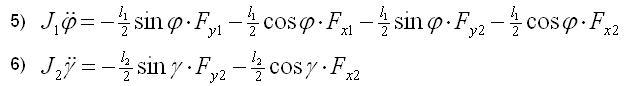
Bild 0-3: Eulergleichungen
Darstellung der Zustandsgrößen und deren erste und zweite Ableitung in Abhängigkeit der Minimalkoordinaten
- Der besseren Übersicht halber werden zunächst folgende Hilfsvariablen eingeführt:
|
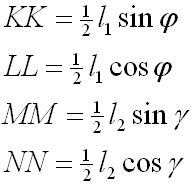
Bild 0-4: Hilfsvariablen
- Als Beziehungen zwischen den Minimalkoordinaten φ und γ und den Schwerpunktskoordinaten ergibt sich dann:
|
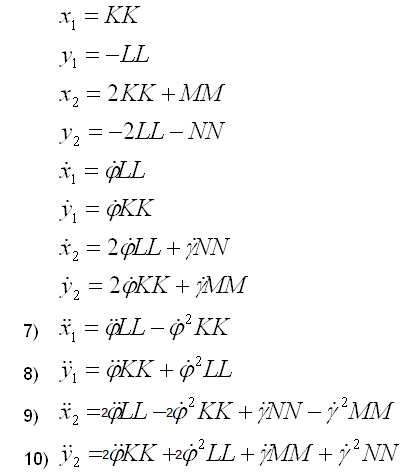
Bild 0-5: Translatorische Zustandsgrößen mit Minimalkoordinaten dargestellt
Aufstellen des LGS zur Berechnung der Zwangskräfte
- Die Gleichugen 5) und 6) werden nach den zweiten Ableitungen von φ und γ aufgelöst.
- Das Ergebnis hiervon wird in 7), 8), 9) und 10) eingesetzt.
- Das Ergebnis hiervon wird für die zweiten Ableitungen von x1, y1, x2, y2 in 1) , 2) , 3) , 4) eingesetzt
- In Matrixschreibweise ergibt sich hieraus folgendes LGS zur Bestimmung der Zwangskräfte:
- Man beachte: Die Zustandsgrößen und deren erste Ableitungen stehen zu einem bestimmten Zeitpunkt, zu dem die Zwangskräfte bestimmt werden zur Verfügung.
|
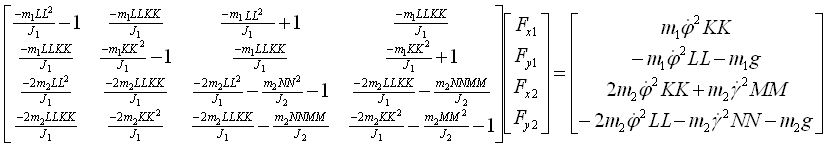
Bild 0-6: LGS zur Bestimmung der Zwangskräfte
- Hinweis: Das LGS der Zwangskräfte wird nicht allgemein gelöst, sondern in jedem Zeitschritt der Integration für konkrete Zahlenwerte mit einem Lösungsverfahren bestimmt.
|
Überführen der Newton-Eulerschen Gleichungen in ein DGLS 1. Grades
- Die Darstellung der Funktion f in dy/dt = f(y,t) kann hier folgendermassen geschehen:
- Hinweis: Die Verwendung der Hilfsvariablen KK, LL, MM, NN eignet sich nicht nur zur kompakteren Darstellung, sondern auch zur Einsparung von Rechenoperationen bei der Simulation.
|
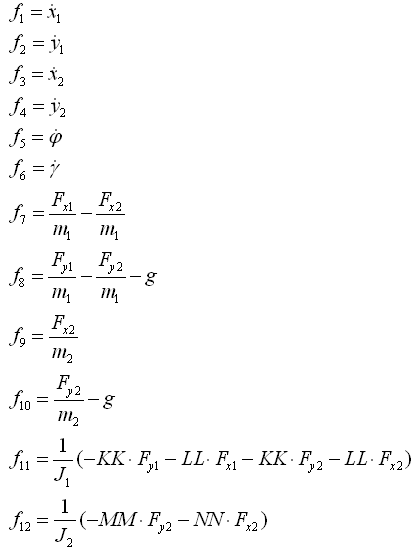
Bild 0-7: Rechte Seite des DGLS
- Das LGS der Zwangskräfte und die Rechte Seite zusammen beschreiben das komplette Modell und sind damit Grundlage für die numerische Integration des Modells.
|
 doppelpendel_vrml.zip - Entwicklung einer Musterlösung für die Animation des Doppelpendels.
doppelpendel_vrml.zip - Entwicklung einer Musterlösung für die Animation des Doppelpendels.