Testen der Möglichkeiten eines Petrinetzes anhand von "Game of Life"
(EN google-translate)
(PL google-translate)
Mit einem Petrinetz "Game of Life" zu implementieren ist sicher eher ein akademisches Beispiel.
Der Vorteil liegt aber darin, die Korrektheit des Verhaltens leicht mittels einer parallelen Implementierung in Javascript vergleichen zu können.
Außerdem stellt es eine gewisse Herausforderung dar, eine nicht ganz triviale Sache umzusetzen.
Hinweise zu "Game of Life"
Von John Horton Conway 1970 entwickeltes "automatisiertes Brettspiel" (zellulärer Automat), bei dem auf ein 2D Raster an beliebigen Plätzen je ein Chip gelegt wird (Anfangskonfiguration) und nach bestimmten Regeln dann Chips verschwinden oder neu entstehen.
Die Regeln:
|
Das Spiel läuft automatisch iterativ durch: Ausgehend von der aktuellen Chipbelegung wird die sich daraus ergebende bestimmt. Letztere wird in einem Zeitschritt eingetragen und auf diese neue wieder die Regeln angewendet usw.
Siehe auch: https://de.wikipedia.org/wiki/Conways_Spiel_des_Lebens
Übung 1
Erstellen Sie ein "Game of Life" auf einem 5x5-Feld mit HTML5/Javascript.
Mögliche Vorlage unter Verwendung von three.js: gol3d004_drehen.html
Alternative mögliche Vorlage unter Verwendung von three.js: ocean_gol007.html
Übung 2
Erstellen Sie ein ein Petrinetz, das die Regeln von "Game of Life" abbildet und wenigstens einen "Blinker" in einem 3x3-Feld realisiert.
Minimale Musterlösung mit Javascript:
<html>
<head lang="de">
<meta charset="iso-8859-1">
<script language:javascript>
const KANTE = 500;
const BREITE = KANTE;
const HOEHE = KANTE;
const RASTER = 11;
const BLOCK = Math.floor(KANTE/RASTER);
const BLOCKRED = Math.floor(BLOCK*0.95);
const OFFSET = Math.floor((BLOCK - BLOCK*0.8)/2);
var matrix;
var matrix_hilf;
var malkontext;
var MAUS_X = 0;
var MAUS_Y = 0;
var SIM = false;
var ZAEHLER = 0;
var SLOWDOWN = 2; //>=1 !!
// 0 1 2 3 4 5 6 7 8 //Anzahl der Nachbarn
var regeln = [1,1,0,2,1,1,1,1,1]; //Bei 0..8 Nachbarn: 0=neutral, 1=tot, 2=geburt
//Hilfsfunktion, die die angeforderten Werte aus der matrix liest, wenn die Ränder verbunden sind.
function gM(k,i)
{
if(k<0)
k+=RASTER;
if(i<0)
i+=RASTER;
k%=RASTER;
i%=RASTER;
return matrix[i][k];
}
function CLEAR()
{
for(var i=0;i<RASTER;i++)
{
for(var k=0;k<matrix.length;k++)
matrix[i][k]=0;
for(var k=0;k<matrix_hilf.length;k++)
matrix_hilf[i][k]=0;
}
}
function malen()
{
//Lazy binding:
//Erst, wenn etwas benötigt wird, wird es bereitgestellt.
if(malkontext==null)
{
var a = '<canvas id="grafik" width="'+BREITE+'" height="'+HOEHE+'"></canvas>';
var b = '<br/><input style="width:200px;text-align:center" type="button" id="START" value="START" onclick="javascript:SIM=true;"/>';
var c = '<br/><input style="width:200px;text-align:center" type="button" id="STOP" value="STOP" onclick="javascript:SIM=false;"/>';
var d = '<br/><input style="width:200px;text-align:center" type="button" id="CLEAR" value="CLEAR" onclick="javascript:CLEAR();"/>';
document.getElementById("BODY").innerHTML = a+b+c+d;
malkontext = document.getElementById("grafik").getContext("2d");
matrix = new Array(RASTER);
matrix_hilf = new Array(RASTER);
for(var i=0;i<RASTER;i++)
{
matrix[i] = new Array(RASTER);
for(var k=0;k<matrix.length;k++)
matrix[i][k]=0;
matrix_hilf[i] = new Array(RASTER);
for(var k=0;k<matrix_hilf.length;k++)
matrix_hilf[i][k]=0;
}
document.getElementById("grafik").addEventListener("mousemove",verarbeiteMaus,false);
document.getElementById("grafik").addEventListener("mousedown",verarbeiteMausklick,false);
setInterval(malen,50);
}
malkontext.fillStyle = "#8888ff";
malkontext.fillRect(0,0,KANTE,KANTE);
for(var i=0;i<RASTER;i++)
{
for(var k=0;k<RASTER;k++)
{
if(matrix[i][k]>0)
malkontext.fillStyle = "#ff0000";
else
malkontext.fillStyle = "#0000ff";
var x = k*BLOCK;
var y = i*BLOCK;
malkontext.fillRect(x+OFFSET,y+OFFSET,BLOCKRED,BLOCKRED);
}
}
if(SIM==true)
{
ZAEHLER++;
if(ZAEHLER%SLOWDOWN==0)
{
for(var i=0;i<RASTER;i++)
{
for(var k=0;k<RASTER;k++)
{
var anzahl_nachbarn = gM(k-1,i-1)+gM(k-0,i-1)+gM(k+1,i-1) +gM(k-1,i+0)+gM(k+1,i+0) +gM(k-1,i+1)+gM(k+0,i+1)+gM(k+1,i+1);
var r = regeln[anzahl_nachbarn];
var w = matrix[i][k];
if(w>0 && r==1)
matrix_hilf[i][k] = 0;
else if(w==0 && r==2)
matrix_hilf[i][k] = 1;
else
matrix_hilf[i][k] = matrix[i][k];
}
}
for(var i=0;i<RASTER;i++)
for(var k=0;k<RASTER;k++)
matrix[i][k] = matrix_hilf[i][k];
}
}
}
function verarbeiteMausklick(event)
{
var i = Math.floor(MAUS_Y/BLOCK);
var k = Math.floor(MAUS_X/BLOCK);
if(matrix[i][k]>0)
matrix[i][k]=0;
else
matrix[i][k]=1;
}
function verarbeiteMaus(event)
{
MAUS_X = event.offsetX;
MAUS_Y = event.offsetY;
}
</script>
</head>
<body style="margin:0; text-align:center">
<span id="BODY" style="margin:0; text-align:center">
<input style="width:200px;text-align:center" type="button" id="snap" value="malen" onclick="javascript:malen()"/>
</span>
</body>
</html>
Code 0-1: Minimale Musterlösung mit Javascript.
Minimale Musterlösung mit PIPE als Petrinetz:
|
gol_musterloesung_petri.zip - Entwicklungsschritte zu einer rudimentären Petri-Netz basierten Umsetzung eines Blinkers in einem 3x3-Netz mit nicht verbundenen Rändern.
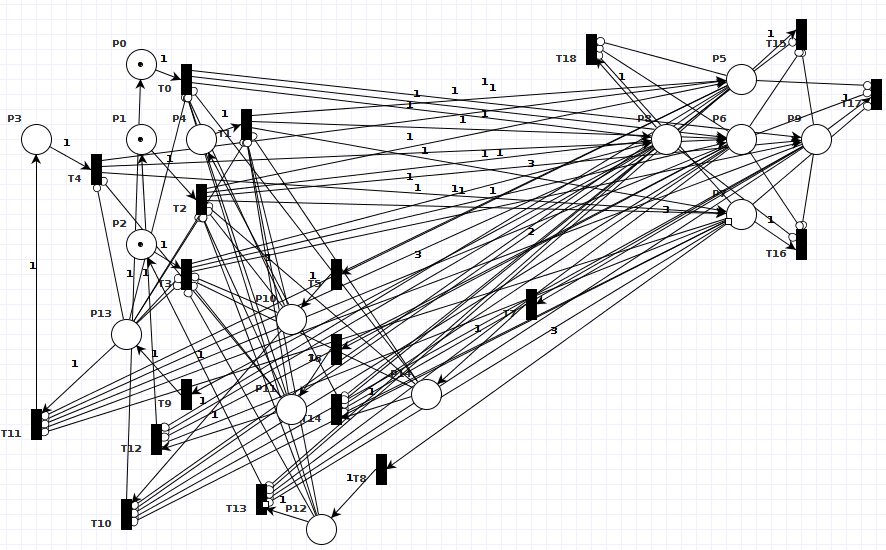
Bild 0-1: Blinker mit Petrinetz.