kramann.info
© Guido Kramann

Snippet Winkelpaar mit dem Arduino 33 nano IoT und am Laptop mit Java/Processing

(EN google-translate)

(PL google-translate)

In den Snippet-Unterkapiteln finden sich kurze, lauffähige Programme, die auf der Basis von IMU und WiFi auf dem Arduino 33 nano IoT in Kombination mit Java/Processing am PC/Laptop bestimmte nützliche Aufgaben erfüllen.

Der Vektor in die Richtung der Erdgravitation, der aus den drei Komponenten des Beschleunigungssensors resultiert soll in zwei orthogonale Winkel alpha und beta umgerechnt werden.
Dabei repräsentiert alpha den Winkel in der x-z-Ebene, der die z-Achse "in die x-Achse dreht, wenn man auf die Spitze der y-Achse schaut".
beta repräsentiert den Winkel in der x-y-Ebene, der die x-Achse "in die y-Achse dreht, wenn man auf die Spitze der z-Achse schaut".
Beide Winkel sind damit im mathematisch positiven Sinne definiert, vergleiche Schaubilder weiter unten.

ACHTUNG: Achsorientierungen mussten gegenüber letztem Snippet teilweise (x/y nicht z) geändert werden.

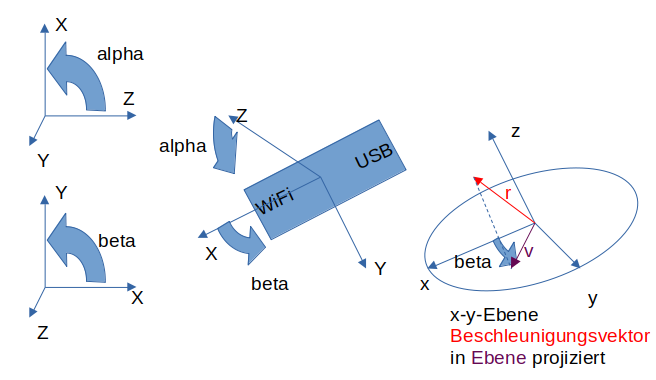
Bild 0-1: Orthogonale Achsen des Beschleunigungssensors bei Ardiono 33 NANO IoT mit Winkelpaar alpha und beta.

Somit muss der Beschleunigungsvektor r in die beiden Ebenen projiziert werden.
Die Projektion in die x-z-Ebene sei Vektor u.
Die Projektion in die x-y-Ebene sei Vektor v (siehe Schaubild oben).
Das Projizieren geht ganz einfach durch weglassen der nicht benötigten Vektorkomponente:

$ \vec r=\left[\begin{array}{cc}x \\ y \\ z\end{array}\right] $

Formel 0-1: Beschleunigungsvektor r

$ \vec u=\left[\begin{array}{cc}x \\ z\end{array}\right] $

Formel 0-2: Projektion von r in die x-z-Ebene ergibt Vektor u.

$ \vec v=\left[\begin{array}{cc}x \\ y\end{array}\right] $

Formel 0-3: Projektion von r in die x-y-Ebene ergibt Vektor v.

Der Cosinussatz besagt, dass für den von zwei Vektoren a und b eingeschlossenen Winkel w gilt, dass dessen Cosinus dem Skalarpodukt der normierten Vektoren a und b entspricht:

$ \cos \left(w\right)= \frac { \vec a \cdot \vec b}{| \vec a| \cdot | \vec b|} $

Formel 0-4: Projektion von r in die x-y-Ebene ergibt Vektor v.

Somit erhält man den Winkel alpha aus folgender Beziehung:

$ \cos \left( \alpha \right)= \frac { \vec u \cdot \vec \left[\begin{array}{cc}0 \\ 1\end{array}\right]}{| \vec u|} $

Formel 0-5: Bestimmungsgleichung für \alpha .

$ \alpha =a \cos \left( \frac {z}{ \sqrt \left(x^2+z^2\right)}\right) $

Formel 0-6: Bestimmungsgleichung für \alpha aufgelöst.

Der Arcuscosinus ist zwischen 0 und 180Grad definiert.
Ist die x-Komponente negativ, so muss vor alpha ein negatives Vorzeichen gesetzt werden.
Beachten Sie auch das Problem, dass der Nenner x^2+z^2 Null werden könnte.

ÜBUNG 1

Leiten Sie analog die Bestimmung des Winkels beta her.
Setzen Sie nun die Berechnung der Winkelpaare aus den Daten des IMU als Processing-Sketch um.
Nutzen Sie als Ausgangspunkt WiFi_IMU_Proc002:

WiFi_IMU_Proc002.zip

WiFi_IMU_Ardu001b.zip -- korresponiderendes Arduino-Programm. Achtung: Hotspot-Adresse anpassen!

ÜBUNG 2

Überlegen Sie vorbereitend auf kommende Woche, wie ZWEI Arduino gleichzeitig benutzt werden könnten.
Analysieren Sie hierzu die Handhabenung der Datenübertragung sowohl im Arduino- als auch im PC-seitigen Programm.
Schreiben Sie einen ersten Programmentwurf.