Die philosophische Sicht auf die menschliche Technik: Was ist Technik? / Was ist das Wesen der Technik?
(EN google-translate)
(PL google-translate)
"Grundlinien einer Philosophie der Technik" von Ernst Kapp (1808-1896)
Wollte man einen geschichtlichen Beginn der Technikphilosophie benennen, so wäre die Arbeit "Grundlinien einer Philosophie der Technik" von Ernst Kapp (1808-1896) zu nennen. Kapp vertritt dort die Ansicht, dass Technik als eine Art "Organprojektionen" gesehen werden kann. Gemeint ist damit, dass technische Artefakte unseren Organen und Gliedmaßen nachempfunden sind. In diesem Sinne könnte man sagen:
|
Die Originalliteratur steht öffentlich bei archive.org zur Verfügung [Kapp]:
Siehe auch [Heßler, S.115-121].
"Hohle Hand" und Schale als ein Beispiel einer Körperprojektion aus Kapp, E., Grundlinien einer Philosophie der Technik, S.56.
ÜBUNG
Übungen werden stets so gehandhabt:
|
|
PRO: Gehhilfe <=> Ersatzbein Verdauungstrakt <=> Ressourcennutzung zur Umwandlung in nutzbarer Energie Sehnen und Bänder <=> Kraftübertragung...Hydraulikschläuche bei Baggern Ohren <=> Hörgeräte Ohren <=> Mikrofon: schwingende Membran Adern <=> Leitungen für Energie usw. Auge <=> Kamera CONTRA: Riechen / Schmecken finden bisher keine technische Nutzung Auto: Wir haben keine Räder Feuer: Nicht zurückführbar auf den Körper Was war zuerst da: Die Nussschale oder die hohle Hand? U-Boot von Wal motiviert Sonar von Wal motiviert Flugzeug: Menschen können nicht fliegen Messer: keine menschliche Entsprechung BEWERTUNG: Vieles aus der Natur wird in die Technik übernommen Aber: Nicht alles wird genutzt beim Körper und es gibt Dinge in der Technik, die nicht auf den Körper zurück geführt können. Fasst man es weiter im Sinne des Wiedererkennens, könnte die ganze Natur Vorbild. Es ist vieles eine Weiterentwicklung Es gibt Lücken, nicht alles kann so abgedeckt werden. Passt zu der Aussage, dass wir nur das erkennen, was wir kennen Kapp hat äußert keine Idee zu einer zukünftigen Entwicklung der Technik
Code 0-1: Studentische Beiträge
"Die Frage nach der Technik" von Martin Heidegger (1889-1976)
"Was im Sinne des Bestandes steht, steht uns nicht mehr als Gegenstand gegenüber" Diese Aussage Martin Heideggers in "Die Technik und die Kehre" [Heidegger 2014, S.16] gibt in kurzen Worten seine Charakterisierung der modernen Technik wieder: Die Dinge sind daran gehindert, sich uns phänomenologisch zu offenbaren, wenn sie für uns als technische Dienstleistung zur Verfügung gestellt sind.
Heidegger erläutert das u.a. am Beispiel eines modernen Staudamms, wenn er beispielsweise im Rhein errichtet würde:
Martin Heidegger, "Die Frage der Technik" in: Martin Heidegger Vorträge und Aufsätze, S.19,20, Klett-Cotta, Stuttgart 2009.
ÜBUNG
|
PRO Wir sind der Auffassung, dass Tiere Pflanzen unsere Ernährungsquellen sind. CONTRA Umwelttechnik dient nicht unserem Nutzen -- aber selbst da steckt letztendlich ein Nutzen für die Menschen Mehrfachnutzung / Staudamm könnte auch Sehenswürdigkeit sein BEURTEILUNG "Der Mensch will aus allem einen Nutzen ziehen" Entwertung des Rheins mit dem Staudamm wird in den Blick genommen -- Ein paar Kilometer weiter ist davon nichts mehr zu sehen. Aber bei Tagebaugebieten wird das ganze Gebiet entwertet. Es ist für nichts mehr gut, als die Energie herauszuholen.
Code 0-2: Studentische Beiträge
Rechentechnik -- Welche Art von Technik ist das?
Husserls "Philosophie der Arithmetik"
Husserls "Philosophie der Arithmetik" [Husserl 1970] stammt aus einer Zeit, bevor er seine phänomenologischen Methode entwickelte.
Der Ausgangspunkt für die Entwicklung der mathematischen Begriffe in diesem Text ist die Menge als ein dem Menschen unmittelbar zugängliches Phänomen.
Allein diese Tatsache sollte eine bewusst phänomenologische Lesart dieses frühen Textes legitimieren, wie sie hier im Folgenden vorgenommen wird. Diese Haltung wird auch durch die Arbeiten von Lohmar [Lohmar] gestützt, und auch durch die Tatsache, dass Husserl wiederum in seinem späteren Werk "Logische Untersuchungen", das Beispiel der gedanklichen Entfaltung mathematischer Ausdrücke bis zur Menge (siehe unten) anführt, um den Unterschied zwischen der unmittelbaren Vorstellung eines Phänomens ("eigentliche Vorstellung eines Phänomens") und einer symbolisch vermittelten Vorstellung ("uneigentliche Vorstellung eines Phänomens") deutlich zu machen [Husserl 2009].
Unsere Vorstellung von Mengen
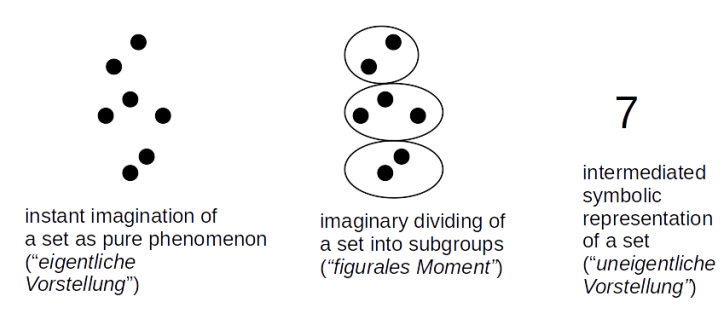
Bild 0-1: Wie wir uns Mengen vorstellen.
Husserl betrachtet Mengen als ein elementares Phänomen. Er betont, dass eine unmittelbare Vorstellung von Mengen möglich ist [Husserl 1970, 201-203], aber nur für sehr kleine Mengen. Und selbst bei sehr kleinen Mengen gelingt es uns noch, sie in Untergruppen aufzuteilen, um ihren Umfang zu erfassen ("figurales Moment") [Husserl 1970, 203-210] (vergl. die Abbildung oben). Im Laufe der Menschheitsgeschichte sind Zahlensysteme zur symbolischen Darstellung von Mengen und auch von mechanisierten Verfahren geworden, die mit diesen Zahlen operieren (Arithmetik), um die verschiedenen Mengen dahinter zu verschmelzen (Addition), mehrere gleich große Mengen zu verschmelzen (Multiplikation) usw. Der Grund dafür liegt nach Husserl in unserem geistigen Unvermögen, diese Operationen direkt an den Mengen durchzuführen [Husserl 1970, 239-240].
Die schrittweise Entfaltung arithmetischer Ausdrücke zu der durch sie repräsentierten Menge
Nach Husserl ist die Menge das elementare Phänomen und die Darstellung von Zahlen im Stellenwertsystem eine symbolische Repräsentation dieser Menge, aus der diese Menge jederzeit wiedergewonnen werden kann. Arithmetische Ausdrücke wiederum sind symbolische Darstellungen, aus denen eine bestimmte Zahl eindeutig gewonnen werden kann. Wie bereits oben erwähnt, erläutert Husserl diese Tatsache auch am Ende des zweiten Teils seiner "Logischen Untersuchungen", um die gegenständliche Bedeutung von Symbolen zu erklären. Er erklärt dies exemplarisch:
Husserl, E., Logische Untersuchungen Teil 2 [Husserl 2009, S.601].
Erfüllungsketten und Phänomene
Im Verlauf der folgenden Ausführungen in [Husserl 2009] verallgemeinert Husserl den hier beschriebenen schrittweisen Prozess der Entfaltung arithmetischer Ausdrücke und postuliert, dass es typischerweise zu einer Steigerung des Inhaltsreichtums führt, wenn man ausgehend von einer gedachten Vorstellung über mehrere Entfaltungsschritte zu einer tatsächlichen Darstellung eines Phänomens gelangt. Ein Beispiel für eine imaginierte Vorstellung könnte die Erinnerung an den Namen einer bestimmten Person sein und die eigentliche Darstellung eines Phänomens könnte dann darin bestehen, sich die Person lebhaft vorzustellen. Der Geltungsbereich dieser Beschreibung soll an dieser Stelle nicht weiter erörtert werden, sondern nur ihre Anwendbarkeit auf den hier interessierenden Bereich. Für diesen Bereich lässt sich ohne Weiteres sagen: Die Umwandlung von symbolischen Ausdrücken in konkretere Vorstellungen ist offensichtlich ein Prozess, bei dem eine Struktur mit relativ wenig Information in eine Struktur mit einer größeren Menge an Information umgewandelt wird. Wird dieser Vorgang mental nachvollzogen, entspricht dies dem von Husserl beschriebenen und von ihm als "Erfüllungsketten" bezeichneten Schema des allmählich zunehmenden Erfülltheitsgrades eines Phänomens.
In diesen Ausführungen insgesamt findet sich zweierlei:
|
|
Beides soll in der folgenden Übung einmal in den Fukus genommen werden:
ÜBUNG
Vorübung: Erstellen Sie selber eine grafische Darstellung zu dem Vorgehen beim Rechnen mit Mengen, wie es von Husserl in den oben zitierten Texten dargestellt wird.
|
zu 1.: Ist das Technik? Ist schon in der Anlage unserer Sinneswahrnehmung angelegt. Zahlensymbole anderer Kulturen? -- CNC Maschinen haben eine Schnittstelle, die mit Koordinaten arbeitet. Programmiersprache legt Bandbreite der Handlungsmöglichkeiten fest zu 2.: Wahrheitsgehalt? zu "Technik denkt nicht" Sammelsurium von Theorien, um die Lebenswelt zu erklären
Code 0-3: Studentische Beiträge
Ein Ausspruch Heideggers ist: "Wissenschaft denkt nicht" -- Wie ordnen Sie den Ausspruch im Zusammenhang mit allem bisher erlernten zu Phänomenologie ein?
Es sind neue Begriffe, die das Potential haben, dasjenige zu erweitern, was man sich vorstellen und unter welchen Gesichtspunkten man etwas beurteilen kann. Es geht hier um die Erweiterung des Begriffshorizont. Es geht weder um abschließende Urteile, noch um das Erreichen einer kohärenten Zusammenschau.
Ergänzungen
Immanuel Kant (1724-1804) hat im Zusammenhang mit der Erkenntnisfähigkeit des Menschen durch sein Werk "Kritik der reinen Vernunft" einige bis heute den philosophischen Diskurs prägende Begriffe eingeführt, wie insbesondere die Begriffspaare "Urteile a priori / a posteriori", sowie "Synthetische und analythische Urteile" [Kant], [Blöser].
Mit diesen Begriffen ist folgendes gemeint:
|
Die für Kant wichtige Frage war, ob synthetische Urteile a priori möglich seien, also ob es möglich sei aus rein geistigen Tatsachen zu Urteilen zu gelangen, die über den Informationsstand davor hinausgehen, ohne dabei neue, weitere äußere Tatsachen zu Rate ziehen zu müssen. Für seine Transzendentale Methodenlehre beantwortet Kant diese Frage positiv und bringt damit eine bis heute andauernde erkenntnistheoretische Debatte in Gang.
| * | Urteile a priori | Urteile a posteriori |
|---|---|---|
| Analythische Urteile | Logiker / Rationalisten | |
| Synthetische Urteile | Metaphysiker | Wissenschaftliche Methode |
Tabelle 0-1: Kombinationsmöglichkeiten von "Urteile a priori / a posteriori", sowie "Synthetische und analythische Urteile" und Vertreter welcher Erkenntnistheorie da jeweils angesiedelt sind, siehe auch: [Hoyningen].
Analythisches Urteil a priori: Alle Menschen sind sterblich. Sokrates ist ein Mensch. Daraus folgt, dass auch Sokrates sterblich ist. (Anwendung der Logik, kein Informationszugewinn) Synthetisches Urteil a posteriori: Versuche mit Sprachaufzeichnungstatsten haben gezeigt: Viele Hunde sind in der Lage eine einfache Sprache zu erlernen, um dann mit Menschen aktiv zu kommunizieren. Synthetisches Urteil a priori: (Mittelalterlicher Gottesbeweis aus Vernunftgründen nach Anselm von Canterbury) ...Ist nicht das Werk eines Malers perfekter als nur der Gedanke daran? Die logische Schlussfolgerung: Wenn wir die Existenz eines vollkommenen Wesens postulieren dann muss es auch existieren. Kurz: Wenn Gott Gott ist, dann ist Gott. Siehe: [Henk]
Code 0-4: (Klassische) Beispiele.
Vergleiche auch:
ÜBUNG
|