Simulations- u. Regelungstechnik im Wintersemester 2025/26
(EN google-translate)
(PL google-translate)
|
|
SRT am Dienstag den 16.11.2025 -- TEIL 1: FUZZY LOGIK, FUZZY SYSTEME, FUZZY REGLER
Themen
|
1. Überblick
In der Lehrveranstaltung Simulations- und Regelungstechnik 2 werden Themen aus der ersten Vorlesung, wie der Zustandsregler, weiter vertieft und Sonderthemen, wie beispielsweise Fuzzy-Regler, neu eingeführt. Auch erhält das Thema Optimierung ein größeres Gewicht.
2. Fuzzy-Logik
 62_Regelungssysteme/18_Fuzzy -- Theorie
62_Regelungssysteme/18_Fuzzy -- Theorie
 62_Regelungssysteme/18_Fuzzy/03_Uebung9 -- Beispiel 1
62_Regelungssysteme/18_Fuzzy/03_Uebung9 -- Beispiel 1
 02_WS2021_22/05_REGmecha5/01_day_by_day -- Beispiel 2
02_WS2021_22/05_REGmecha5/01_day_by_day -- Beispiel 2
 72_COACH2/12_Fuzzy/01_Uebungsaufgabe -- Übung
72_COACH2/12_Fuzzy/01_Uebungsaufgabe -- Übung
 80_Robuste_Systemintegration/10_EvoFuzzy -- Preview: Aufbau von Fuzzy-Reglern und deren Optimierung über Evolutionäre Algorithmen
80_Robuste_Systemintegration/10_EvoFuzzy -- Preview: Aufbau von Fuzzy-Reglern und deren Optimierung über Evolutionäre Algorithmen
3. Fuzzy-Regler

Bild 0-1: Beispiel für einem Fuzzy-Regler.
Übung: Ersetze den Zustandsregler unten durch einen Fuzzy-Regler

Bild 0-2: Umzusetzender Fuzzy-Regler (gleiche Geometrie wie oben, aber andere Regeln und erweitertes Ausgangsfuzzyset)
clear;
function F = fregler(x,v)
F = -x-v;
endfunction
function f = rechteSeite(t,y)
x = y(1,1);
v = y(2,1);
F = fregler(x,v);
f(1,1) = v;
f(2,1) = -x + F;
endfunction
t = 0:0.01:10;
y0 = [2,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-1: Rahmensystem, in dem der Zustandsregler durch die Implementierung eines Fuzzy-Reglers ersetzt werden soll.
clear;
function nzp = fuzzysetX(x)
endfunction
function nzp = fuzzysetV(v)
endfunction
function F = fregler(x,v)
// 1. Fuzzifizieren der Eingangsgrößen x und v, heißt: zu jeder Fuzzygröße
// jedes der beiden Eingangsfuzzysets wird der Erfülltheitsgrad berechnet.
nzp_x = fuzzysetX(x);
nzp_v = fuzzysetX(v);
// 2. Erfülltheitsgrade jeder Regel berechnen
erfuelltheit = zeros(9);
erfuelltheit(1) = min(nzp_x(1),nzp_v(1));
//...
// 3. Defuzzifizierung der Ausgangsgröße (Kraft F), heißt Schwerpunktberechnung.
endfunction
function f = rechteSeite(t,y)
x = y(1,1);
v = y(2,1);
F = fregler(x,v);
f(1,1) = v;
f(2,1) = -x + F;
endfunction
t = 0:0.01:10;
y0 = [2,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-2: Noch unfertige Umsetzung, jedoch mit kompletter Programmstruktur.
clear;
function A=flaecheTrapez(h)
q = 2.0;
p = 2.0*(1.0-h);
A = h*(p+q)/2.0;
end
function nzp = fuzzysetX(x)
nzp = zeros(3);
if x<-1 then
nzp(1)=1.0;
nzp(2)=0.0;
nzp(3)=0.0;
elseif x<0 then
nzp(1)=-x;
nzp(2)=1-nzp(1);
nzp(3)=0.0;
elseif x<1 then
nzp(3)=x;
nzp(2)=1-nzp(3);
nzp(1)=0;
else
nzp(1)=0.0;
nzp(2)=0.0;
nzp(3)=1.0;
end
endfunction
function nzp = fuzzysetV(v)
nzp = zeros(3);
if v<-1 then
nzp(1)=1.0;
nzp(2)=0.0;
nzp(3)=0.0;
elseif v<0 then
nzp(1)=-v;
nzp(2)=1-nzp(1);
nzp(3)=0.0;
elseif v<1 then
nzp(1)=0.0;
nzp(3)=v;
nzp(2)=1-nzp(3);
else
nzp(1)=0.0;
nzp(2)=0.0;
nzp(3)=1.0;
end
endfunction
function erg=mini(x,y)
if x<y then
erg=x;
else
erg=y;
end
end
function F = fregler(x,v)
// 1. Fuzzifizieren der Eingangsgrößen x und v, heißt: zu jeder Fuzzygröße
// jedes der beiden Eingangsfuzzysets wird der Erfülltheitsgrad berechnet.
nzp_x = fuzzysetX(x);
nzp_v = fuzzysetV(v);
// 2. Erfülltheitsgrade jeder Regel berechnen
ef = zeros(9); //erfuelltheit
ef(1) = mini(nzp_x(1),nzp_v(1)); //Regel 1
ef(2) = mini(nzp_x(2),nzp_v(1)); //Regel 2
ef(3) = mini(nzp_x(3),nzp_v(1)); //...
ef(4) = mini(nzp_x(1),nzp_v(2));
ef(5) = mini(nzp_x(2),nzp_v(2));
ef(6) = mini(nzp_x(3),nzp_v(2));
ef(7) = mini(nzp_x(1),nzp_v(3));
ef(8) = mini(nzp_x(2),nzp_v(3));
ef(9) = mini(nzp_x(3),nzp_v(3));
//...
//F = F/Ages;
// 3. Defuzzifizierung der Ausgangsgröße (Kraft F), heißt Schwerpunktberechnung.
F=0.0;
Ages=0.0;
sp=[2,1,0,1,0,-1,0,-1,-2];
//Regel 1..9:
for i=1:9
A=flaecheTrapez(ef(i));
s=sp(i);
Ages=Ages+A;
F=F+s*A;
end
F=F/Ages;
endfunction
function f = rechteSeite(t,y)
x = y(1,1);
v = y(2,1);
F = fregler(x,v);
f(1,1) = v;
f(2,1) = -x + F;
endfunction
t = 0:0.01:10;
y0 = [2,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-3: Komplettes System.
4. Übungen
Aufgabe 1
Am Eingang eines Fuzzy-Systems liegen folgende Werte an: x=2, y=-1
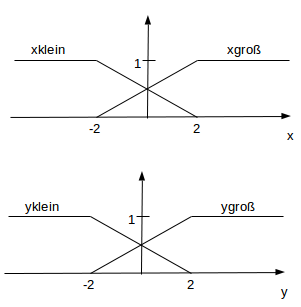
Bild 0-3: Fuzzy-System.
Die Fuzzy-Regeln lauten:
r1: WENN xgross UND ygross DANN Fklein r2: WENN xgross UND yklein DANN Fklein r3: WENN xklein UND ygross DANN Fgross r4: WENN xklein UND yklein DANN Fgross
Code 0-4: Fuzzy-Regeln
Geben Sie den Erfülltheitsgrad zu jeder Regel an.
r1=... r2=... r3=... r4=...
Code 0-5: Erfülltheitsgrad zu jeder Regel.
Aufgabe 2
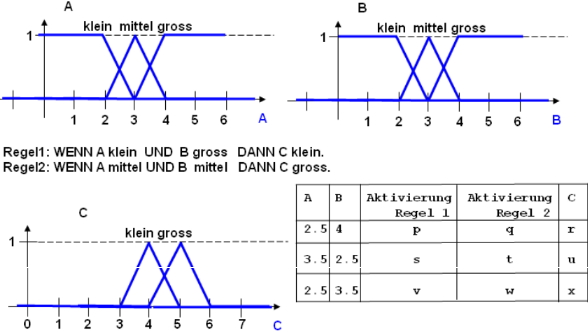
Bild 0-4: Fuzzy-System.
|
SRT am Dienstag den 16.11.2025 -- TEIL 2: OBJEKTORIENTIERTE PROGRAMMIERUNG
|
Studentische Lösung
clear;
mode(0);
clc;
A=3.5;
B=2.5;
function a = SystemA(A)
if A<=2 then
a(1)=1;
a(2)=0;
a(3)=0;
end
if A>2 && A<=3 then
a(1)=-A+3;
a(2)=A-2;
a(3)=0;
end
if A>3 && A<=4 then
a(1)=0;
a(2)=-A+4;
a(3)=A-3;
end
if A>4 then
a(1)=0;
a(2)=0;
a(3)=1;
end
endfunction
function b = SystemB(B)
if B<=2 then
b(1)=1;
b(2)=0;
b(3)=0;
end
if B>2 && B<=3 then
b(1)=-B+3;
b(2)=B-2;
b(3)=0;
end
if B>3 && B<=4 then
b(1)=0;
b(2)=-B+4;
b(3)=B-3;
end
if B>4 then
b(1)=0;
b(2)=0;
b(3)=1;
end
endfunction
function A=flaecheTrapez(h)
q = 2.0;
p = 2.0*(1.0-h);
A = h*(p+q)/2.0;
end
function C = berechneC (A,B)
a=SystemA(A);
b=SystemB(B);
Reg1=min(a(1),b(3));
Reg2=min(a(2),b(2));
A1=flaecheTrapez(Reg1);
A2=flaecheTrapez(Reg2);
s1=4;
s2=5;
C=(s1*A1+s2*A2)/(A1+A2);
pause;
endfunction
C=berechneC(A,B);
Code 0-6: Studentische Lösung zu Aufgabe 2.
1. Einführung in Java-Processing
 78_Processing
78_Processing
 SRT001.zip -- Lösung zu Aufgabe 2 oben mit Java-Procressing.
SRT001.zip -- Lösung zu Aufgabe 2 oben mit Java-Procressing.
public class Vektor
{
double x,y;
public double berechneLaenge()
{
return Math.sqrt(x*x+y*y);
}
}
public void setup()
{
Vektor v1,v2;
v1 = new Vektor();
v2 = new Vektor();
v1.x = 3.0;
v1.y = 4.0;
v2.x = 1.0;
v2.y = 0.0;
println("Länge v1: "+v1.berechneLaenge());
println("Länge v2: "+v2.berechneLaenge());
}
public void draw()
{
}
Code 0-7: Konzept der Objektorientierung am Beispiel des mathematischen R2-Vektors
 SRT003.zip -- Aufgabe 2 in Klasse gepackt.
SRT003.zip -- Aufgabe 2 in Klasse gepackt.
 SRT004.zip -- Einsatz der Konstruktormethode.
SRT004.zip -- Einsatz der Konstruktormethode.
2. Einführung in die Objektorientierte Programmierung mit Java-Processing
 Allgemein: 30_Informatik3/01_Vom_struct_zur_Klasse/06_Objektabstraktion
Allgemein: 30_Informatik3/01_Vom_struct_zur_Klasse/06_Objektabstraktion
SRT am Montag den 24.11.2025 -- Fortsetzung TEIL 2: OBJEKTORIENTIERTE PROGRAMMIERUNG
|
1. Paradigmen der Objektorientierten Programmierung und UML
...vergl. Vorlesung / werden anhand der nachfolgenden Beispiele erläutert:
|
 30_Informatik3/02_UML
30_Informatik3/02_UML
 30_Informatik3/02_UML/02_UML_Klassendiagramm
30_Informatik3/02_UML/02_UML_Klassendiagramm
 30_Informatik3/02_UML/03_Konstruktor
30_Informatik3/02_UML/03_Konstruktor
 30_Informatik3/19_UML_ALT/02_UML_Flaechenberechnung
30_Informatik3/19_UML_ALT/02_UML_Flaechenberechnung
 30_Informatik3/19_UML_ALT/04_ListeUML
30_Informatik3/19_UML_ALT/04_ListeUML
 30_Informatik3/02_UML/04_Statische_Variable
30_Informatik3/02_UML/04_Statische_Variable
 30_Informatik3/03_Strings/02_stringUML
30_Informatik3/03_Strings/02_stringUML
 30_Informatik3/06_Vererbung/01_MesswerteUML
30_Informatik3/06_Vererbung/01_MesswerteUML
 30_Informatik3/06_Vererbung/03_VererbungsProgramm
30_Informatik3/06_Vererbung/03_VererbungsProgramm
NACHTRAG: Der Modifikator "protected" in C++:
 "protected" in C++: 30_Informatik3/07_Modifikatoren/02_protected_Vererbung
"protected" in C++: 30_Informatik3/07_Modifikatoren/02_protected_Vererbung
2. Schnittstellen / Interfaces am Beispiel eines Simulationsprogramms
 73_COACH3/09_Algorithmen -- Spezielle Implementierungen von Modell und Integrator genügen deren allgemeinerer Spezifikation durch Interfaces.
73_COACH3/09_Algorithmen -- Spezielle Implementierungen von Modell und Integrator genügen deren allgemeinerer Spezifikation durch Interfaces.
 73_COACH3/09_Algorithmen/01_RungeKutta -- Prozedurale Umsetzung als Vorstufe zum Verständnis.
73_COACH3/09_Algorithmen/01_RungeKutta -- Prozedurale Umsetzung als Vorstufe zum Verständnis.
 73_COACH3/09_Algorithmen/02_Loesungsansatz -- Ansatz in Java auf der Grundlage von Vererbung.
73_COACH3/09_Algorithmen/02_Loesungsansatz -- Ansatz in Java auf der Grundlage von Vererbung.
 78_Processing/06_Snippets/15_Simulation -- Beispielimplementierung mit Runge Kutta Integrator mit Processing.
78_Processing/06_Snippets/15_Simulation -- Beispielimplementierung mit Runge Kutta Integrator mit Processing.
Nachfolgendes Projekt wird ausführlich im Unterricht besprochen und bildet die Grundlage für alle weiteren OOP-Projekte:
 Simulator002.zip -- Vollständiges Simulationsprogramm, implementiert mit Processing unter Verwendung von Interfaces.
Simulator002.zip -- Vollständiges Simulationsprogramm, implementiert mit Processing unter Verwendung von Interfaces.
Ergänzung: Interfaces mit C++
ÜBUNG
Aufgabe 1
|
 Simulator005_Euler.zip -- studentische Lösung.
Simulator005_Euler.zip -- studentische Lösung.
Aufgabe 2
Unter nachfolgendem Link unter "Musterlösung zu Übung 2 vom 15.12.2020" finden Sie eine vollständige Herleitung zum invertierenden Pendel und eine Umsetzung mit Scilab:
 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21 -- "Musterlösung zu Übung 2 vom 15.12.2020"
62_Regelungssysteme/98_day_by_day_WS2021_SoSe21 -- "Musterlösung zu Übung 2 vom 15.12.2020"
|
3. Planung der objektorientierten Implementierung eines Fuzzy-Reglers
Im Hinblick darauf, einen Fuzzy-Regler für das invertierende Pendel auf der Basis von Processing zu entwerfen und zu optimieren, soll folgende Vorarbeit geleistet werden:
|
Nachfolgende Punkt vorr. in nachfolgenden Lehrveranstaltungen:
4. Vergleich: Objektorientierte Programmierung mit Java und C/C++
 C++: 30_Informatik3/01_Vom_struct_zur_Klasse/03_Klassen_Programm
C++: 30_Informatik3/01_Vom_struct_zur_Klasse/03_Klassen_Programm
5. Einführung in Android-Processing
 93_Android_Proc
93_Android_Proc
 77_Android
77_Android
6. Einrichtung eines Hotspots unter Linux und unter Android, oder mittels eines Routers
 Vernetzung mehrerer Geräte: 92_Soundinstallation/03_material/11_Snippets/11_UDP
Vernetzung mehrerer Geräte: 92_Soundinstallation/03_material/11_Snippets/11_UDP
Hotspot Android Device
 05_esp32AV/01_Bauanleitung/01_Elektronik_und_Software/03_Videostream
05_esp32AV/01_Bauanleitung/01_Elektronik_und_Software/03_Videostream
Hotspot Linux Computer
 08_Archiv/06_Ing/01_Bauplan/04_Hotspot
08_Archiv/06_Ing/01_Bauplan/04_Hotspot
W-LAN-Router
 siehe ganz unten!: Einrichtung am Beispiel von tp-link-W-LAN-Routern: 05_esp32AV/01_Bauanleitung/03_FAQs
siehe ganz unten!: Einrichtung am Beispiel von tp-link-W-LAN-Routern: 05_esp32AV/01_Bauanleitung/03_FAQs
7. Programmierung von Anwendungen mit UDP
 Internetprogrammierung -- 67_Echtzeitsysteme/09_Internetprogrammierung/04_Java
Internetprogrammierung -- 67_Echtzeitsysteme/09_Internetprogrammierung/04_Java
SRT am Montag den 25.11.2025 -- Fortsetzung OOP / Einachser Simulation / Optimierung / Fuzzy-Regler
Themen
|
1. Hinweise zu OOP -- siehe Projekt Simulator002.zip
|
2. Plotter-Klasse
 Simulator006_Plotter.zip -- Plotfunktion in einer Klasse abbilden.
Simulator006_Plotter.zip -- Plotfunktion in einer Klasse abbilden.
ÜBUNG
|
|
3. Implementierung Einachser-Modell
 Simulator007_Einachser.zip
Simulator007_Einachser.zip
 Grundlage bildet: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, siehe dort "Musterlösung zu Übung 2 vom 15.12.2020"
Grundlage bildet: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, siehe dort "Musterlösung zu Übung 2 vom 15.12.2020"
4. Regler als Extraklasse
 Simulator008_Regler.zip -- Vereinbarung einer Schnittstelle für einen Regler / Umsetzung des Zustandsreglers
Simulator008_Regler.zip -- Vereinbarung einer Schnittstelle für einen Regler / Umsetzung des Zustandsreglers
5. Regleroptimierung mittels Gradientenverfahren
|
 Simulator009_Fehlerfunktion.zip -- Fehlerfunktuion für den Zustandsregler des Einachsers.
Simulator009_Fehlerfunktion.zip -- Fehlerfunktuion für den Zustandsregler des Einachsers.
ÜBUNG
public interface iOptimierer
{
public abstract void configure(iFehlerfunktion fehlerfunktion, double[] startparameter);
public abstract void iteration();
public abstract double[] getBestParametersatz();
}
Code 0-8: Interface für einen Optimierer
|
6. Gemeinsamer Entwurf eines Fuzzy-Reglers
|
ÜBUNG
|
public void setup()
{
}
public interface iEingangsFuzzySet
{
/**
breite ist der Abstand zwischen der am weitesten links liegenden Fuzzy-Größe und
der am weitesten rechts liegenden.
Alle Fuzzy-Größen werden äquidistant angeordnet.
*/
public abstract void setzeStuetzpunkte(double breite);
/** Liefert Erfülltheitsgrad einer bestimmten Fuzzy-Größe */
public abstract double berechneErfuelltheitsgrad(int index, double x);
}
public interface iAusgangsFuzzySet
{
/** breite reicht hier bis an die Berührpunkte der äußeren Dreiecke mit der x-Achse */
public abstract void setzeStuetzpunkte(double breite);
/**
int[][] regeln: jede Eingangsgröße der beiden E.-Fuzzysets mit jeder kombiniert beeinflusst
eine Fuzzy-Größe des Ausgangsfuzzysets. Letztere ist im Array eingetragen als Index.
double[][] aktivierungen: aktuell aus der Eingangssituation resultierende Aktivierungen jeder
Regel korrespondierend mit int[][] regeln.
*/
public abstract double berechneSchwerpunkt(int[][] regeln, double[][] aktivierungen);
}
public interface iFuzzySystem
{
public abstract double berechneAusgang(double[] y);
/** obere neue Breiten für Eingangsfuzzysets, unterste ist die Breite für das Ausgangsfuzzyset */
public abstract void setzeBreiten(double[] breiten);
}
Code 0-9: Definition der Schnittstellen für ein Fuzzy-System, das in Processing umgesetzt werden soll.
SRT am Montag den 01.12.2025
|
1. Einführung in die Optimierung
 Optimierung, Einführung -- 50_Simulationstechnik/06_Optimierung
Optimierung, Einführung -- 50_Simulationstechnik/06_Optimierung
 Heuristiken -- 50_Simulationstechnik/06_Optimierung/02_Heuristiken
Heuristiken -- 50_Simulationstechnik/06_Optimierung/02_Heuristiken
 Gradientenverfahren -- 50_Simulationstechnik/06_Optimierung/01_Gradientenverfahren
Gradientenverfahren -- 50_Simulationstechnik/06_Optimierung/01_Gradientenverfahren
 Modifiziertes Gradientenverfahren -- 50_Simulationstechnik/06_Optimierung/03_ModifizierteG
Modifiziertes Gradientenverfahren -- 50_Simulationstechnik/06_Optimierung/03_ModifizierteG
 optim() in Scilab -- 50_Simulationstechnik/06_Optimierung/04_optim
optim() in Scilab -- 50_Simulationstechnik/06_Optimierung/04_optim
function F = fehlerfunktion(u)
x = u(1);
y = u(2);
F = x^3-4*x+y^3-16*y
endfunction
ustart = [1,1];
uopt = [2/sqrt(3),4/sqrt(3) ]
Fstart = fehlerfunktion(ustart)
Fopt = fehlerfunktion(uopt)
alfa = 0.01;
schritte = 1000
u=ustart;
Fakt=fehlerfunktion(u)
for i=1:schritte
r = floor(grand(2, 1, "unf", 0, 2.999999999))-1;
uneu = u + alfa*(r');
Fneu = fehlerfunktion(uneu);
if Fneu<Fakt
Fakt = Fneu;
u=uneu;
end
end
disp("Endergebnis der Optimierung:")
disp(u)
disp("Fehler am Ende:")
disp(fehlerfunktion(u))
Code 0-10: Modifiziertes Gradientenverfahren mit Scilab.
//Alfa steuern
function F = fehlerfunktion(u)
x = u(1);
y = u(2);
F = x^3-4*x+y^3-16*y
endfunction
ustart = [1,1];
uopt = [2/sqrt(3),4/sqrt(3) ]
Fstart = fehlerfunktion(ustart)
Fopt = fehlerfunktion(uopt)
alfa = 0.1;
alfaunterschwelle=0.003;
schritte = 100
u=ustart;
Fakt=fehlerfunktion(u)
//for i=1:schritte
while alfa>alfaunterschwelle
r = floor(grand(2, 1, "unf", 0, 2.999999999))-1;
uneu = u + alfa*(r');
Fneu = fehlerfunktion(uneu);
if Fneu<=Fakt //wenn sich nichts ändert, trotzdem wandern!!!
Fakt = Fneu;
u=uneu;
alfa=alfa*1.1;
else
alfa=alfa*0.9;
end
end
disp("Endergebnis der Optimierung:")
disp(u)
disp("Fehler am Ende:")
disp(fehlerfunktion(u))
disp("Alfa am Ende:")
disp(alfa);
Code 0-11: Modifiziertes Gradientenverfahren mit Schrittweitensteuerung.
2. Wie kann man das machen? -- Snippets und Hilfsfunktionen zur Bewältigung der Programmieraufgaben
Vorschläge:
|
3. Fortsetzung der Übungsaufgaben, im Anschluss Arbeiten an den Projekten
 Simulator010_Optimierer.zip
Simulator010_Optimierer.zip
 Simulator011_Optimierer.zip
Simulator011_Optimierer.zip
ÜBUNG
|
 Simulator012_Optimierer.zip
Simulator012_Optimierer.zip
ÜBUNG
 FuzzySystem001.zip
FuzzySystem001.zip
|
 FuzzySystem002.zip -- Musterlösung.
FuzzySystem002.zip -- Musterlösung.
SRT am Dienstag den 02.12.2025
Themen:
|
1. Fortsetzung zur Entwicklung eines Fuzzy-Systems mit Processing
 FuzzySystem003.zip -- Vollständige aber nicht getestete Implementierung
FuzzySystem003.zip -- Vollständige aber nicht getestete Implementierung
2. Vorbesprechung der Übungen
3. ÜBUNGEN
Aufgabe 1 -- Wdh. Kleinste Quadrate Methode
VoltCm = [ 2.5 20
2.0 30
1.5 40
1.05 60
0.75 90
0.5 130
0.45 150
];
// Aufgabe:
// a) Messwerte möglichst gut durch quadratische Funktion annähern
// b) Messwerte möglichst gut durch kubische Funktion annähern
// Verläufe aus a) , b) und den Messwerten übereinander als Plot darstellen
// a) und b) sind mit Scilab mittels kleinster Quadrate-Methode zu lösen.
Code 0-12: Näherung der Meßwerte zu einem Entfernungssensor über Funktionen
Aufgabe 2 -- Parameterstudie
|
 Grundlage bildet wieder: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, siehe dort "Musterlösung zu Übung 2 vom 15.12.2020"
Grundlage bildet wieder: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21, siehe dort "Musterlösung zu Übung 2 vom 15.12.2020"
clear();
clc();
m = 1; //kg
g = 0.91; // m/s^2
l = 1; // m
h = l/2; // m
r = 0.1; // m
J = 0.25*m*r*r + (1/12)*m*l*l; // kg*m^2
xstart = 2.0;
xende = 3.0;
ystart = 0.0;
yende = 1.0;
schritte = 10;
err = ones ();
for v=1:5
//Fehler in Kombinationen berechnen:
c = 1;
xdivide = (xende-xstart)/schritte;
xschritte = xstart:xdivide:xende;
ydivide = (yende-ystart)/schritte;
yschritte = ystart:ydivide:yende;
for w = 1:size(xschritte,'c')
xmoment = xschritte(w);
r=1;
for u = 1:size(yschritte,'c')
ymoment = yschritte(u);
R = [xmoment ymoment];
function f = rechteSeite(t,y)
phi = y(1,1);
om = y(2,1);
f(1,1) = om;
FA = -R * [phi;om];
N = J + m*h*h*sin(phi)*sin(phi);
f(2,1) = (-m*h*h*om*om*sin(phi)*cos(phi) + h*m*sin(phi)*g + h*cos(phi)*FA )/N;
endfunction
t = linspace(0,20,3000);
y0 = [10.0*%pi/180,0.0]'; //Start in der Nähe der instabilen Ruhelage
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
for i=1:3000
errPHI = y(1,i)*y(1,i);
errOM = y(2,i)*y(2,i);
end
errPHI = sqrt(errPHI);
errOM = sqrt(errOM);
err(r,c) = errPHI + errOM;
r=r+1;
end
c = c+1;
end
//kleinsten Fehler suchen und neue Start/Ende setzten:
[minimum,klein] = min(err);
xwert = klein(1,1);
ywert = klein(1,2);
if xwert == schritte+1 then
xstart = xschritte(xwert-1);
xende = xschritte(xwert);
elseif xwert == 1 then
xstart = xschritte(1);
xende = xschritte(xwert+1);
else
xstart = xschritte(xwert-1);
xende = xschritte(xwert+1);
end
if ywert == schritte+1 then
ystart = yschritte(ywert-1);
yende = yschritte(ywert);
elseif ywert == 1 then
ystart = yschritte(1);
yende = yschritte(ywert+1);
else
ystart = yschritte(ywert-1);
yende = yschritte(ywert+1);
end
end
R = [xschritte(xwert) yschritte(ywert)];
function f = rechteSeite1(t,y)
phi = y(1,1);
om = y(2,1);
f(1,1) = om;
FA = -R * [phi;om];
N = J + m*h*h*sin(phi)*sin(phi);
f(2,1) = (-m*h*h*om*om*sin(phi)*cos(phi) + h*m*sin(phi)*g + h*cos(phi)*FA )/N;
endfunction
t = linspace(0,20,3000);
y0 = [10.0*%pi/180,0.0]'; //Start in der Nähe der instabilen Ruhelage
t0 = 0;
y = ode(y0,t0,t,rechteSeite1);
subplot(1,2,1);
plot(t,y(1,:)',t,y(2,:)');
title("neu");
s
//ursprünglicher Code:
A = [ 0 , 1 ; m*g*h/J , 0 ];
B = [ 0 ; h/J ];
spec(A) //Eigenwerte der ursprünglichen Matrix ansehen
// ergibt:
// 2.3023837 + 0.i
// -2.3023837 + 0.i
// technisch stabil wählen, an vorhandenen Werten orientieren:
EW = [-2.3023837 + %i*2.3023837 , -2.3023837 - %i*2.3023837 ];
Ru = ppol(A,B,EW)
// ergibt (korrigiert 5.1. wg. verändertem B):
// 2.7299999 0.7904851
function f = rechteSeite2(t,y)
phi = y(1,1);
om = y(2,1);
f(1,1) = om;
FA = -Ru * [phi;om];
N = J + m*h*h*sin(phi)*sin(phi);
f(2,1) = (-m*h*h*om*om*sin(phi)*cos(phi) + h*m*sin(phi)*g + h*cos(phi)*FA )/N;
endfunction
t = linspace(0,20,3000);
y0 = [10.0*%pi/180,0.0]'; //Start in der Nähe der instabilen Ruhelage
t0 = 0;
y = ode(y0,t0,t,rechteSeite2);
subplot(1,2,2);
plot(t,y(1,:)',t,y(2,:)');
title("ursprünglich");
Code 0-13: Studentische Lösung.
Aufgabe 3 -- Vorstudie Evolutionäre Algorithmen
|
|
|
import java.util.Random;
Random zufall = new Random(System.currentTimeMillis());
public int[][] erzeugeZufallsmatrix(int zeilen, int spalten)
{
int[][] arr = new int[zeilen][spalten];
for(int i=0;i<arr.length;i++)
for(int k=0;k<arr[i].length;k++)
arr[i][k] = zufall.nextInt(2);
return arr;
}
public void showArray(int[][] arr)
{
println();
for(int i=0;i<arr.length;i++)
{
for(int k=0;k<arr[i].length;k++)
{
print(arr[i][k]+" ");
}
println();
}
}
public void drawArray(int[][] arr, float x, float y, float w)
{
float d = w/(float)arr.length;
noStroke();
for(int i=0;i<arr.length;i++)
{
for(int k=0;k<arr[i].length;k++)
{
if(arr[i][k]>0)
fill(0);
else
fill(255);
rect(x+(float)k*d,y+(float)i*d,w,w);
}
}
}
public void setup()
{
size(600,600);
frameRate(5);
int[][] x = erzeugeZufallsmatrix(8, 8);
showArray(x);
}
public void draw()
{
background(255);
int[][] x = erzeugeZufallsmatrix(16, 16);
drawArray(x, 0, 0, width);
}
Code 0-14: Hilfsprogramm.
Aufgabe 4 -- Verifizierung der FuzzySystem-Software FuzzySystem003
|
1. Eingangsfuzzyset: 3 Fuzzygrößen Breite: 2.0 2. Eingangsfuzzyset: 3 Fuzzygrößen Breite: 2.0 Ausgangsfuzzyset: 3 Fuzzygrößen Breite: 4.0 Regelmatrix: 0 1 2 1 2 0 2 0 1
Code 0-15: Zu erzeugendes Fuzzy-System
|
in1=1 in2=0 in1=1 in2=1 in1=0.5 in2=0.5 in1=0.75 in2=1.0
Code 0-16: Stichproben.
|
Aufgabe 5 -- Fuzzy-Regler für das invertierende Pendel
|
Die Ergenisse dieser Aufgaben werden im nachgang diskutiert werden und dann umgesetzt.
SRT am Montag den 08.12.2025 -- Fortsetzung OOP / Einachser Simulation / Optimierung / Fuzzy-Regler
Themen
|
1. OOP mit Java
|
Die Main-Klasse bei Java -- Untersuchung eines regulären Java-Anwendungsprogramms
 36_Java
36_Java
 36_Java/01_GettingStarted -- Siehe Code 0-1.
36_Java/01_GettingStarted -- Siehe Code 0-1.
 java_konsolen_projekt.zip -- Java-Anwendung in Terminal kompilieren und starten.
java_konsolen_projekt.zip -- Java-Anwendung in Terminal kompilieren und starten.
|
 Hallo001.zip -- Exportierter Sketch.
Hallo001.zip -- Exportierter Sketch.
Vererbung mit Java
 Hallo002.zip -- Vektor als innere Klasse.
Hallo002.zip -- Vektor als innere Klasse.
 Hallo003.zip -- Nebenläufiger Prozess mittels Schnittstelle (interface)
Hallo003.zip -- Nebenläufiger Prozess mittels Schnittstelle (interface)
|
Das Singleton-Pattern und seine Realisierung als statische Klasse in Java und in C++ bei der Mikrocontroller-Programmierung
 40_Mikrocontroller/08_OOP/03_Statisch -- Statische Methoden mit C++ bei der Mikrocontroller-Programmierung.
40_Mikrocontroller/08_OOP/03_Statisch -- Statische Methoden mit C++ bei der Mikrocontroller-Programmierung.
jar und javadoc
Das Erzeugen und Einbinden von Java-Bibliotheken (.jar-Files), aber auch die automatische Erstellung von Dokumentationen mit Hilfe von javadoc wird beispielsweise in der Entwicklungsumgebung bluej direkt unterstützt, siehe beispielsweise:
 93_Android_Proc/02_Eigene_Library
93_Android_Proc/02_Eigene_Library
 93_Android_Proc/03_Crossplattform
93_Android_Proc/03_Crossplattform
2. Besprechung zu Aufgabe 4 -- Verifizierung der FuzzySystem-Software FuzzySystem003
|
p= 0.5
q= 0.0
r= 4.0
s= 0.0
t= 0.5
u= 5.0
v= 0.5
w= 0.5
x= 4.5
Code 0-17: Musterlösung für die geforderten Werte.
|
 FuzzySystem004.zip -- Musterlösung.
FuzzySystem004.zip -- Musterlösung.
public void setup()
{
double[] OFFSETS = {3.0,3.0,4.5};
double[] breiten = {2.0,2.0,3.0};
int[] anzahlFuzzyGroessen = {3,3,2};
int[][] regeln = {
{-1,-1, 0}, // -1 => fehlende Regel!
{-1, 1,-1},
{-1,-1,-1}
};
//FuzzySystem(double[] OFFSETS, double[] breiten, int[] anzahlFuzzyGroessen, int[][] regeln)
FuzzySystem fs = new FuzzySystem(OFFSETS,breiten,anzahlFuzzyGroessen,regeln);
println("p="+fs.berechneAktivierung(new double[] {2.5,4.0}, 0, 2));
println("q="+fs.berechneAktivierung(new double[] {2.5,4.0}, 1, 1));
println("r="+fs.berechneAusgang(new double[] {2.5,4.0}));
println("s="+fs.berechneAktivierung(new double[] {3.5,2.5}, 0, 2));
println("t="+fs.berechneAktivierung(new double[] {3.5,2.5}, 1, 1));
println("u="+fs.berechneAusgang(new double[] {3.5,2.5}));
println("v="+fs.berechneAktivierung(new double[] {2.5,3.5}, 0, 2));
println("w="+fs.berechneAktivierung(new double[] {2.5,3.5}, 1, 1));
println("x="+fs.berechneAusgang(new double[] {2.5,3.5}));
}
Code 0-18: setup-Methode der Musterlösung.
SRT am Montag den 09.12.2025 -- Fortsetzung OOP / Einachser Simulation / Optimierung / Fuzzy-Regler
Themen
|
1. Implmementierung eines Fuzzy-Reglers für den Einachser
2. Optimierung des Fuzzy-Reglers für den Einachser
 Simulator013_Fuzzy.zip -- Musterlösung.
Simulator013_Fuzzy.zip -- Musterlösung.
Ersetzt werden musste:
|
Das vorbereitete Fuzzy-System wird Teil des Reglers.
public class FuzzyRegler implements iRegler
{
double FMAX = 0.0;
FuzzySystem fs;
public FuzzyRegler()
{
//FuzzySystem(double[] breiten, int[] anzahlFuzzyGroessen, int[][] regeln)
double[] breiten = {1.0,1.0,1.0};
int[] anzahlFuzzyGroessen = {5,5,5};
// -- - 0 + ++
// 0 1 2 3 4
int[][] regeln = {
{ 4, 4, 3,-1,-1},
{ 4, 3, 3,-1,-1},
{-1, 3, 2, 1,-1},
{-1,-1, 1, 1, 0},
{-1,-1, 1, 0, 0}
};
fs = new FuzzySystem(breiten, anzahlFuzzyGroessen, regeln);
}
public double berechneStellgroesseU(double[] y)
{
double phi = y[0];
double om = y[1];
//double FA = -R[0]*phi - R[1]*om;
double FA = fs.berechneAusgang(y);
if(FA<FMAX)
{
FMAX=FA;
//println("FA="+FA);
}
if(FA>0.4) FA=0.4;
if(FA<-0.4) FA=-0.4;
return FA;
}
public void setParameter(double[] param)
{
fs.setzeBreiten(param);
}
}
Code 0-19: Implementierung des Fuzzy-Reglers.
public class FehlerfunktionFuzzyregler implements iFehlerfunktion
{
Simulator simulator;
iRegler regler;
double[][] yt; //letzte Zeile: t Verlauf
double dt;
public FehlerfunktionFuzzyregler()
{
regler = new FuzzyRegler();
simulator = new Simulator(new RungeKuttaIntegrator(),new Einachser(regler));
dt = 20.0/3000.0; // 20 Sekunden, 3000 Schritte
yt=simulator.exec(dt, 3000, 0.0, new double[] {10.0*Math.PI/180,0.0});
}
public double berechneFehler(double[] param)
{
regler.setParameter(param);
yt=simulator.exec(dt, 3000, 0.0, new double[] {10.0*Math.PI/180,0.0});
double errPHI = 0.0;
double errOM = 0.0;
for(int i=0;i<yt[0].length;i++)
errPHI+=yt[0][i]*yt[0][i];
errPHI = Math.sqrt(errPHI);
for(int i=0;i<yt[1].length;i++)
errOM+=yt[1][i]*yt[1][i];
errOM = Math.sqrt(errOM);
return errPHI + errOM;
}
}
Code 0-20: Implementierung der Fehlerfunktion.
3. Fehlerfunktion für das Rorschachproblem
4. Evolutionärer Optimierer für das Rorschachproblem
ÜBUNG
 R002_Fehlerfunktion.zip -- Teillösung
R002_Fehlerfunktion.zip -- Teillösung
Erweitern und verbessern Sie die Teillösung:
|
 R004_Mutation_Zusammenhang.zip -- Lösung aus verschiedenen studentischen Lösungen kombiniert.
R004_Mutation_Zusammenhang.zip -- Lösung aus verschiedenen studentischen Lösungen kombiniert.
Themen Probe-E-Test morgen (16.12.2025)
|
...dazu kommt in der Klausur noch:
|
SRT am Dienstag den 15.12.2025
Themen
|
1. Proboe-E-Test
2. Wiederholung Zustandsregler
 62_Regelungssysteme/08_Polvorgabe
62_Regelungssysteme/08_Polvorgabe
 62_Regelungssysteme/12_Adaptiv/06_Zustandsregler
62_Regelungssysteme/12_Adaptiv/06_Zustandsregler
3. Zustandsregler mit Beobachter
 62_Regelungssysteme/09_Beobachter
62_Regelungssysteme/09_Beobachter
 62_Regelungssysteme/12_Adaptiv/07_Beobachter
62_Regelungssysteme/12_Adaptiv/07_Beobachter
4. Koordinatentransformation für zustandsregler, die nicht auf Null ausregeln sollen
 62_Regelungssysteme/08_Polvorgabe
62_Regelungssysteme/08_Polvorgabe