Modellbildung und Simulationstechnik als Anwendung
(EN google-translate)
(PL google-translate)
Gottfried-Wilhelm Leibniz (1646-1716) sagte, die Natur mache keine Sprünge und fing damit an, natürliche Vorgänge durch Differentialgleichungen zu beschreiben. Damit war die moderne Simulationstechnik geboren.
Themen
|
1. Einführung in Modellbildung, Simulationstechnik und numerischer Mathematik
|
2. Mathematisches Modell eines Feder-Masse-Schwingers
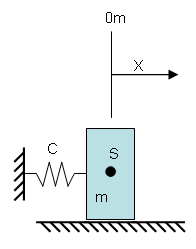
Bild 0-1: Skizze zum Feder-Masse-Schwinger.
$ m \ddot x=-Cx $
Formel 0-1: Lineare Differentialgleichung & die ein Simulationsmodell des Feder-Masse-Schwingers darstellt.
Das Newtonsche Gesetz besagt: "Die Impulsänderung ergibt sich aus der Summe der an einen starren Körper angreifenden Kräfte." Im vorliegenden Fall steht links der Gleichung die Änderung des Impulses und rechts davon die angreifende Federkraft. Man kann die Gleichung auch so umschreiben ...
$ \ddot x=- \frac {C}{m}x $
Formel 0-2: Lineare Differentialgleichung & die ein Simulationsmodell des Feder-Masse-Schwingers darstellt umgeschrieben.
... um sich klar zu machen, dass durch die angreifende Kraft eine Beschleunigung auf die Masse wirkt.
|
3. Das Euler Integrationsverfahren
|
$ \dot x=f\left(x\right) $
Formel 0-3: Explizite lineare Differentialgleichung erster Ordnung.
...gegeben, so kann man das Differential in einen Differenzenquotienten überführen und die Gkeichung nach dem neu zu berechnenden Wert auflösen:
$ \frac { \Delta x}{ \Delta t}=f\left(x\right) $
Formel 0-4: Differenzenquotient statt Differential.
$ \frac {xneu - xalt}{tneu - talt}=f\left(xalt\right) $
Formel 0-5: Auflösen des Differenzenquotienten.
$ xneu=xalt + f\left(xalt\right) \cdot \delta t $
Formel 0-6: Iterative Bestimmungsgleichung für den jeweils einen Zeitschritt nachfolgenden Wert.
In Worten: "Der neue Wert ergibt sich angenähert, wenn man zu dem alten Wert die aktuelle Steigung mal die Zeitschrittweite addiert."
Der Feder-Masse-Schwinger lässt sich mit einem Trick in die zur Anwendung des Euler-Verfahrens notwendige Form bringen:
$ \ddot x=- \frac {C}{m}x $
Formel 0-7: Ausgangspunkt.
$ \dot x=v $
Formel 0-8: Substitutionsgleichung.
$ \dot v=- \frac {C}{m}x $
Formel 0-9: Schwinger-Gleichung unter Ausnutzung der Substitutionsbeziehung.
Man erhält auf diese Weise zwei Differentialgleichungen erster Ordnung aus ursprünglich einer Differentialgleichung zweiter Ordnung.
4. main-Programm des Simulationsmodells eines Feder-Masse-Schwingers
|
|
...Das bedeutet: Wir lenken die Masse aus der Ruhe um einen Meter aus und lassen dann los, kann man sagen.
#include <iostream>
using namespace std;
int main(void)
{
double m = 1.0; //Masse 1kg
double C = 1.0; //Federkonstante 1N/m
double dt= 0.01; //Zeitschrittweite delta t = 0,01s
double xalt = 1.0; //Anfangsbedingung x0=1m
double valt = 0.0; //Anfangsbedingung v0=0m/s
double xneu; //Die jeweils neu berechneten Werte der Simulationsgrößen x und v
double vneu; //
double t = 0.0; //Die aktuelle Zeit, die seit Start der Simulation vergangen ist.
double tend = 10.0; //Die Simulation soll nach 10 Sekunden beendet werden.
while(t<tend)
{
xneu = xalt + valt*dt;
vneu = valt - (C/m)*xalt*dt;
cout<<"t="<<t<<" x="<<xalt<<"m v="<<valt<<"m/s"<<endl;
xalt = xneu;
valt = vneu;
t=t+dt;
}
return 0;
}
Code 0-1: Simulationsprogramm federmasse.cpp ausgeführt als main-Methode in C/C++.
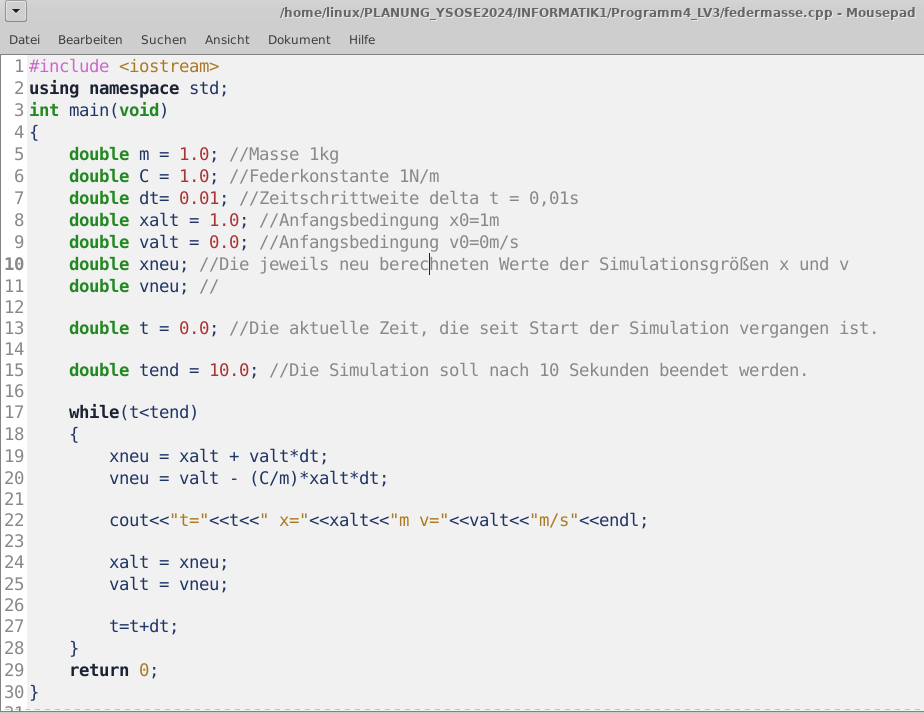
Bild 0-2: Screenshot des Quelltextes zum Simulationsprogramm mit Zeilenangaben zur Besprechung im Unterricht.
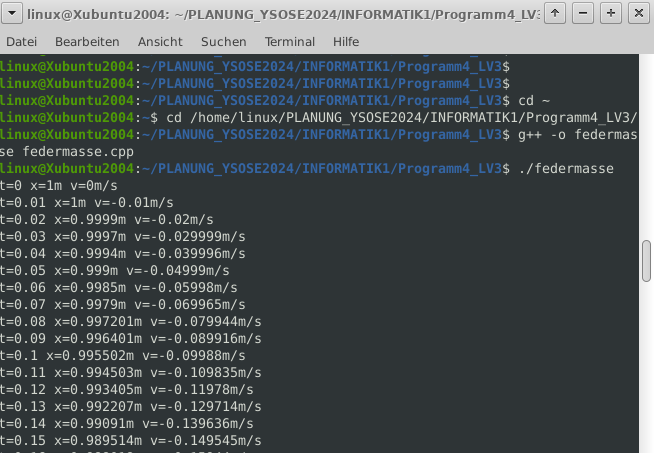
Bild 0-3: Eingaben in das Terminal, um das Programm zu kompilieren und zu starten.
5. Plotten des zeitlichen Verlaufs der Variablen des Simulationsmodells mit Hilfe von Scilab
|
|
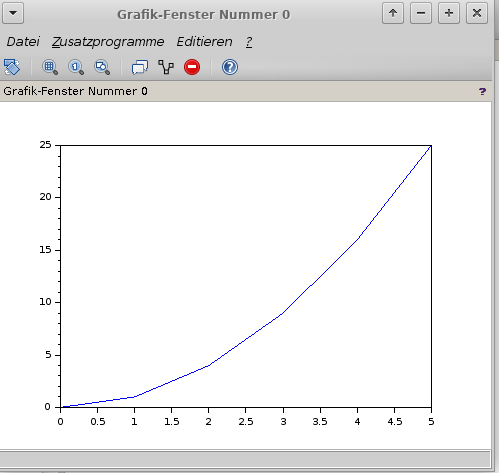
Bild 0-4: Testplot mit Scilab.
|
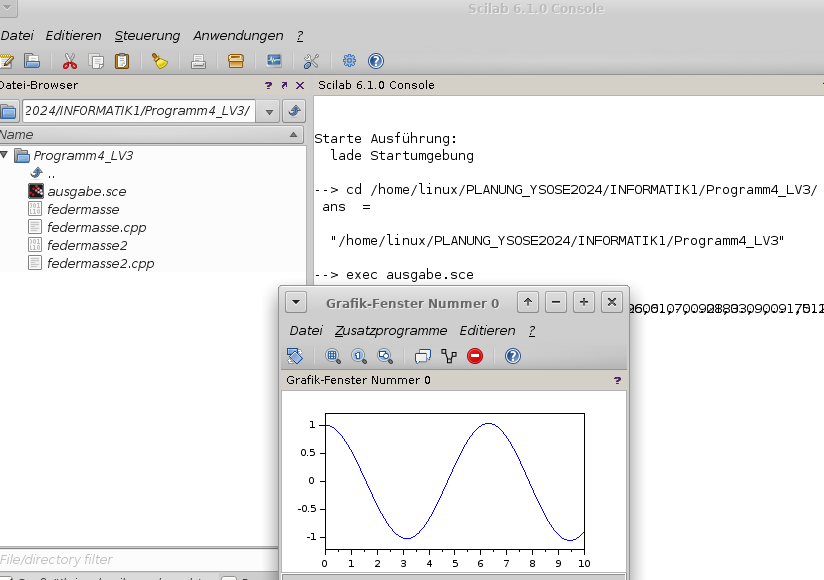
Bild 0-5: Darstellung von Scilab und dem Plot aus ausgabe.sce.
Das Script ausgabe.sce wurde mit Hilfe des folgenden C/C++-Programms erzeugt:
#include <iostream>
using namespace std;
int main(void)
{
double m = 1.0; //Masse 1kg
double C = 1.0; //Federkonstante 1N/m
double dt= 0.01; //Zeitschrittweite delta t = 0,01s
double xalt = 1.0; //Anfangsbedingung x0=1m
double valt = 0.0; //Anfangsbedingung v0=0m/s
double xneu; //Die jeweils neu berechneten Werte der Simulationsgrößen x und v
double vneu; //
double t = 0.0; //Die aktuelle Zeit, die seit Start der Simulation vergangen ist.
double tend = 10.0; //Die Simulation soll nach 10 Sekunden beendet werden.
cout<<"plot([";
while(t<tend)
{
cout<<t;
if(t<=tend-dt)
{
cout<<",";
}
t=t+dt;
}
cout<<"],[";
t=0.0;
while(t<tend)
{
xneu = xalt + valt*dt;
vneu = valt - (C/m)*xalt*dt;
cout<<xalt;
if(t<=tend-dt)
{
cout<<",";
}
xalt = xneu;
valt = vneu;
t=t+dt;
}
cout<<"]);"<<endl;
return 0;
}
Code 0-2: Simulationsprogramm federmasse2.cpp des Feder-Masse-Schwingers mit einer Ausgabe, die in Scilab als Plot-Befehl interpretiert werden kann.
6. Funktionen in C/C++
Vor allem in dem zuletzt präsentierten C/C++-Programm werden mehrere Dinge in einem erledigt:
|
Dadurch wird das Programm langsam etwas intransparent: Man versteht wenn man darauf blickt nicht mehr so leicht, was es macht. Außerdem lassen sich die genannten verschiedenen Aufgaben, die erledigt werden auch schwer voneinander trennen.
Eine Möglichkeit, Einzelaufgaben, die erledigt werden sollen voneinander zu trennen und einen stärker modularisierten Aufbau eines Programms zu erzielen, stellt die Verwendung von Funktionen dar.
|
Das nachfolgende Beispiel beinhaltet das gleiche Programm ohne und mit Verwendung einer Funktion. In der dritten Variante wird außerdem eine Schleife verwendet.
#include <iostream>
using namespace std;
int main(void)
{
double x,y;
x=1.0;
y=x*x;
cout<<"x="<<x<<" y="<<y<<endl;
x=2.0;
y=x*x;
cout<<"x="<<x<<" y="<<y<<endl;
x=3.0;
y=x*x;
cout<<"x="<<x<<" y="<<y<<endl;
return 0;
}
Code 0-3: p1.cpp
#include <iostream>
using namespace std;
double quadrat(double z)
{
return z*z;
}
int main(void)
{
double x,y;
x=1.0;
y=quadrat(x);
cout<<"x="<<x<<" y="<<y<<endl;
x=2.0;
y=quadrat(x);
cout<<"x="<<x<<" y="<<y<<endl;
x=3.0;
y=quadrat(x);
cout<<"x="<<x<<" y="<<y<<endl;
return 0;
}
Code 0-4: p2.cpp
#include <iostream>
using namespace std;
double quadrat(double z)
{
return z*z;
}
int main(void)
{
double x;
x=1.0;
while(x<=3.0)
{
cout<<"x="<<x<<" y="<<quadrat(x)<<endl;
x=x+1.0;
}
return 0;
}
Code 0-5: p3.cpp
7. Modularisierung des Berechnungsprogramms durch Verwendung von Funktionen
|
#include <iostream>
using namespace std;
//Substitutionsgleichung
double berechneSteigung1(double v)
{
double xpunkt = v;
return xpunkt;
}
//Zweite Differentialgleichung
double berechneSteigung2(double x)
{
double C = 1.0;
double m = 1.0;
double vpunkt = -(C/m)*x;
return vpunkt;
}
//Euler Integrationsverfahren
double berechneNaechstenWert(double alterWert, double aktuelleSteigung, double dt)
{
return alterWert + aktuelleSteigung*dt;
}
int main(void)
{
double dt= 0.01; //Zeitschrittweite delta t = 0,01s
double xalt = 1.0; //Anfangsbedingung x0=1m
double valt = 0.0; //Anfangsbedingung v0=0m/s
double xneu; //Die jeweils neu berechneten Werte der Simulationsgrößen x und v
double vneu; //
double t = 0.0; //Die aktuelle Zeit, die seit Start der Simulation vergangen ist.
double tend = 10.0; //Die Simulation soll nach 10 Sekunden beendet werden.
cout<<"plot([";
while(t<tend)
{
cout<<t;
if(t<=tend-dt)
{
cout<<",";
}
t=t+dt;
}
cout<<"],[";
t=0.0;
while(t<tend)
{
xneu = berechneNaechstenWert(xalt, berechneSteigung1(valt),dt);
vneu = berechneNaechstenWert(valt, berechneSteigung2(xalt),dt);
cout<<xalt;
if(t<=tend-dt)
{
cout<<",";
}
xalt = xneu;
valt = vneu;
t=t+dt;
}
cout<<"]);"<<endl;
return 0;
}
Code 0-6: federmasse3.cpp
|
#include <iostream>
#define SIMULATIONSSCHRITTE 1000
using namespace std;
//Simulationsmodell
void berechneSteigung(double *st,double *y)
{
double C = 1.0;
double m = 1.0;
st[0] = y[1];
st[1] = -(C/m)*y[0];
}
//Euler Integrationsverfahren
void euler(double *yneu, double *yalt, double dt)
{
double st[2];
berechneSteigung(st,yalt);
yneu[0] = yalt[0] + st[0]*dt;
yneu[1] = yalt[1] + st[1]*dt;
}
//Simulation
void simulation(double *y, int anz, double dt, double x0,double v0)
{
double yneu[2],yalt[2];
yalt[0]=x0;
yalt[1]=v0;
for(int i=0;i<anz;i++)
{
y[i]=yalt[0]; //merken des x-Wertes in einem Array
euler(yneu, yalt, dt);
yalt[0]=yneu[0];
yalt[1]=yneu[1];
}
}
void printScilabVector(double *y,int anz)
{
cout<<"[";
for(int i=0;i<anz;i++)
{
cout<<y[i];
if(i<anz-1)
cout<<",";
}
cout<<"]";
}
void printScilabVector(int anz, double start, double delta)
{
cout<<"[";
for(int i=0;i<anz;i++)
{
cout<<start;
if(i<anz-1)
cout<<",";
start+=delta;
}
cout<<"]";
}
int main(void)
{
double y[SIMULATIONSSCHRITTE];
int anz = sizeof(y)/sizeof(double);
//cout<<(sizeof(y)/sizeof(double))<<endl;
simulation(y,anz, 0.01, 1.0,0.0);
cout<<"t=";
printScilabVector(anz, 0.0, 0.01);
cout<<";"<<endl;
cout<<"y=";
printScilabVector(y,anz);
cout<<";"<<endl;
cout<<"plot(t,y);"<<endl;
return 0;
}
Code 0-7: federmasse4.cpp
8. Übungsaufgaben
Aufgabe 1
|
Aufgabe 2
|
Aufgabe 3
|
$ m \ddot x=-Cx-D \dot x $
Formel 0-10: Lineare Differentialgleichung & die ein Simulationsmodell des Feder-Masse-Dämpfer-Systems darstellt.
|