kramann.info
© Guido Kramann

Informatik -- Lehrveranstaltung vom 22.05.2024

(EN google-translate)

(PL google-translate)

Everything Everywhere All at Once

... angelehnt an den gleichnamigen Film, erschien mir das ein passender Titel dafür, dass nun alles, was bislang behandelt wurde innerhalb eines größeren Projektes verwendet wird.

Ein Simulationsprogramm eines linearen Schwingers soll zunächst wiederholend mit C/C++ umgesetzt werden.
Im Anschluss wird das Projekt nach Java/Processing objektorientiert übertragen.
Schließlich wird eine Animation der Echtzeitsimulation umgesetzt, dessen Kernstück in einer von der Klasse Modell erbenden Erweiterung implementiert wird.
ÜBUNG: Variation aller Teilprojekte in 1.,2.,3.: Umsetzung des Räuber-Beute-Modells.

1. Simulationsprogramm in C/C++ quasi als Wiederholung, aber unter Verwendung von Funktionen

Dieses war die Grundstruktur eines Differentialgleichungssystems erster Ordnung, das beispielsweise mittels des Euler-Integrationsverfahrens numerisch gelöst werden kann:

$ \vec \dot y = \vec f\left( \vec y\right) $

Formel 0-1: Differentialgleichungssystem erster Ordnung.

Dies ist ein konkretes Beispiel für ein in dem Fall lineares Differentialgelichungssystem erster Ordnung, ein linearer Feder-Dämpfer-Masse-Schwinger:

$ \left[\begin{array}{cc}\dot x \\ \dot v\end{array}\right] = \left[\begin{array}{cc}v \\ -x-0.3 \cdot v\end{array}\right] $

Formel 0-2: Linearer Feder-Dämpfer-Masse-Schwinger mit konkreten Parametern.

Anfangsbedingungen werden gewählt zu: x0=1m, v0=0m/s mit Teitschrittweite dt=0.01s.

Im Vergleich hierzu, auch mit konkreten Parametern, ist nachfolgend das Differentialgleichungssystem des Räuber-Beute-Modells dargestellt:

$ \left[\begin{array}{cc}\dot B \\ \dot R\end{array}\right]=\left[\begin{array}{cc}B-0.01 \cdot B \cdot R \\ -R+0.01 \cdot B \cdot R\end{array}\right] $

Formel 0-3: Räuber-Beute-Modell mit konkreten Parametern.

Anfangsbedingungen werden gewählt zu: B0=100, R0=10 mit Teitschrittweite dt=0.01Jahre.

Eine einfache Umsetzung in C/C++ der Simulation des Schwingers wäre:

#include <iostream>
using namespace std;
int main(void)
{
    double tmax=10.0;
    double dt=0.01;
    double t=0.0;
    double x0=1.0;
    double v0=0.0;
    double x=x0;
    double v=v0;
    
    int anzahl = 0;
    while(t<tmax)//Zählen, wieviele Datenelemente benötigt werden.
    {
        anzahl++;
        t+=dt;
    }

    double arrt[anzahl];
    double arrx[anzahl];
    double arrv[anzahl];

    t=0.0;

    for(int i=0;i<anzahl;i++)
    {
        arrt[i]=t;
        arrx[i]=x;
        arrv[i]=v;

        double xneu = x + (v)*dt;
        double vneu = v + (-x-0.3*v)*dt;

        x=xneu;
        v=vneu;

        t+=dt;
    }

    //Ausgabe für Scilab:
    cout<<"t=[";
    for(int i=0;i<anzahl;i++)
    {
        cout<<arrt[i];
        if(i<anzahl-1) cout<<",";
    }
    cout<<"];"<<endl;

    cout<<"x=[";
    for(int i=0;i<anzahl;i++)
    {
        cout<<arrx[i];
        if(i<anzahl-1) cout<<",";
    }
    cout<<"];"<<endl;

    cout<<"v=[";
    for(int i=0;i<anzahl;i++)
    {
        cout<<arrv[i];
        if(i<anzahl-1) cout<<",";
    }
    cout<<"];"<<endl;

    cout<<"plot(t,x,\'blu\',t,v,\'gre\');"<<endl;

    return 0;
}

Code 0-1: schwinger.cpp

NEU: Die Daten werden in Scilab als Arrays dargestellt.

Das Programm kann folgendermaßen kompiliert werden:
g++ -o schwinger schwinger.cpp 
Um die Ausgabe in ein Scilab-Skript umzuleiten, kann so vorgegangen werden:
./schwinger > sim.sce
Innerhalb von Scilab wird mit cd in den richtigen Pfad navigiert.
exec sim.sce führt dann das Skript aus.

Code 0-2: Hinweise zur Umsetzung.

Scilab erzeugt dann folgenden Plot:

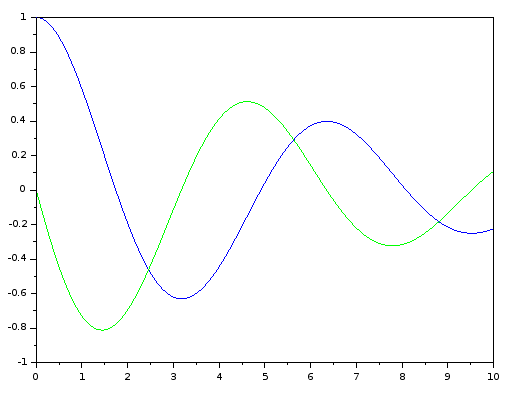
Bild 0-1: In Scilab erzeugter Plot zur Simulation.

Wie können geschickt Funktionen eingesetzt werden, um den Quelltext besser zu strukturieren und Redundanzen zu vermeiden?

Umsetzung erfolgt im Unterricht!

#include <iostream>
using namespace std;

void printScilabArray(char variablenname, double array[],int anzahl)
{
    //Ausgabe für Scilab:
    cout<<variablenname<<"=[";
    for(int i=0;i<anzahl;i++)
    {
        cout<<array[i];
        if(i<anzahl-1) cout<<",";
    }
    cout<<"];"<<endl;
}

int main(void)
{
    double tmax=10.0;
    double dt=0.01;
    double t=0.0;
    double x0=1.0;
    double v0=0.0;
    double x=x0;
    double v=v0;
    
    int anzahl = 0;
    while(t<tmax)//Zählen, wieviele Datenelemente benötigt werden.
    {
        anzahl++;
        t+=dt;
    }

    double arrt[anzahl];
    double arrx[anzahl];
    double arrv[anzahl];

    t=0.0;

    for(int i=0;i<anzahl;i++)
    {
        arrt[i]=t;
        arrx[i]=x;
        arrv[i]=v;

        double xneu = x + (v)*dt;
        double vneu = v + (-x-0.3*v)*dt;

        x=xneu;
        v=vneu;

        t+=dt;
    }

    //Ausgabe für Scilab:
    printScilabArray('t',arrt,anzahl);
    printScilabArray('x',arrx,anzahl);
    printScilabArray('v',arrv,anzahl);

    cout<<"plot(t,x,\'blu\',t,v,\'gre\');"<<endl;

    return 0;
}

Code 0-3: Einsatz einer Funktion, um den Code effizienter zu machen.

2. Objekt orientierte Übertragung des Simulationsprogramms auf Java/Processing

Hier soll eine Echtzeitsimulation umgesetzt werden.
Die Zeitschrittweite wird auf dt=0.02 gesetzt und passend dazu die Frame-Rate auf 50 Frames pro Sekunde.
Es werden die Klassen Modell und Integrator gebildet.
Die Klasse Integrator ermöglicht das Euler-Integrationsverfahren.
Die Klasse Modell repräsentiert den linearen Schwinger.

Integrator integrator;

public void setup()
{
     size(640,480);
     frameRate(50);
     
     integrator = new Integrator(new Modell());
}

double x=1.0;
double v=0.0;
double dt=0.02;
double[] y = new double[] {x,v};

public void draw()
{
    background(255);
    double[] yneu = integrator.step(y,dt);
    
    fill(255,0,0);
    ellipse(width/2,height/2.0f+(float)yneu[0]*200.0f,50,50);
    
    y[0]=yneu[0];
    y[1]=yneu[1];
}

Code 0-4: Hauptprogramm.

public class Modell
{
     public double[] berechneSteigung(double[] y)
     {
         double x = y[0];
         double v = y[1];
         
         double steigung_x = v;
         double steigung_v = -x-0.3*v;
         
         double[] steigung = {steigung_x, steigung_v};
         
         return steigung;
     }
}

Code 0-5: Klasse Modell.

public class Integrator
{
    Modell modell;
    
    public Integrator(Modell modell)
    {
        this.modell = modell;
    }
    
    public double[] step(double[] y, double dt)
    {
        double[] steigung = modell.berechneSteigung(y);

        double[] yneu = new double[steigung.length];
        
        for(int i=0;i<yneu.length;i++)
            yneu[i] = y[i] + steigung[i]*dt;
            
        return yneu;    
    }
}

Code 0-6: Klasse Integrator.

Download des Processing-Projektes Schwinger101.zip.

3. Erweiterung der Klasse Modell um eine Visualisierungsmöglichkeit

Umsetzung im Unterricht!

ModellVis erweitert die Klasse Modell, indem eine draw-Methode ergänzt wird.
Im ersten Schritt muss dafür gesorgt werden, dass der aktuelle Zustand für draw verfügbar bleibt.
Im zweiten Schritt soll die gleiche Visualisierung erfolgen, wie zuvor in draw().
Schließlich soll eine realistischere Darstellung mit sich dehnender Feder und rechteckiger grauer Masse umgesetzt werden.

4. ÜBUNG

8.1. Kleine Aufgaben

Aufgabe 8.1.1

Schreiben Sie auswendig ein Hello-World-Programm in C/C++ und testen und nötigenfalls korrigieren es.
Schreiben Sie auswendig ein Hello-World-Programm mit Java/Processing. Die Ausgabe soll mittels der text(..)-Methode auf dem Fenster erfolgen.

public void setup()
{
    size(640,480);
}

public void draw()
{
    background(255,0,0);
    fill(0,255,0);
    textSize(50);
    textAlign(CENTER);
    text("Hello World!",width/2,height/2);
}

Code 0-7: Mögliche Lösung eines Hello-World-Programms mit Processing.

Aufgabe 8.1.2

Schreiben Sie in C/C++ eine Funktion getMinimum(...), der man ein Double-Array übergibt und die den darin befindlichen kleinsten Wert zurück gibt und testen Sie die Funktion durch Aufruf aus einer main-Funktion heraus.
Schreiben Sie in Java/Processing eine Klasse Messwerte, die als Objektmethode auch die getMinimum()-Methode enthält. Die Messwerte (Array mit double-Werten) sollen hier Objekt-Attribut sein, so, dass der getMinimum()-Methode hier kein Array von Außen übergeben werden muss.
Zeichnen Sie ein UML-Klassendiagramm zu der Klasse Messwerte.

public class Messwerte
{
     double[] arr = {3.7,6.4,39.3,7.0};
     
     public double getMinimum()
     {
         double min = arr[0];
         for(int i=0;i<arr.length;i++)
            if(arr[i]<min)
               min = arr[i];
         return min;      
     }
}
public void setup()
{
     Messwerte mess = new Messwerte();
     double ergebnis = mess.getMinimum();
     println("Minimum ist:"+ergebnis);    
}

Code 0-8: Simple Java-Lösung.

public class Messwerte
{
     double[] arr = new double[1000];
     int anzahl=0;
     public void add(double x)
     {
         arr[anzahl]=x;
         anzahl++;
     }
     
     public double getMinimum()
     {
         double min = arr[0];
         for(int i=0;i<anzahl;i++)
            if(arr[i]<min)
               min = arr[i];
         return min;      
     }
}
public void setup()
{
     Messwerte mess = new Messwerte();
     Messwerte mess2 = new Messwerte();
     mess.add(3.9);
     mess.add(-3.9);
     mess.add(1.9);
     mess2.add(-7.9);
     mess2.add(-0.9);
     mess2.add(0.9);
     double ergebnis = mess.getMinimum();
     println("Minimum bei mess ist:"+ergebnis);    
     println("Minimum bei mess2 ist:"+mess2.getMinimum());    
}

Code 0-9: Beispiellösung zur Java-Version mit zwei Messwert-Objekten.

Aufgabe 8.1.3

Wiederholen von cin und cout, Schreiben Sie ein C/C++-Programm mit folgender Funktion:
Ausgabe eines Hinweises für den Benutzer, wie das Programm zu verwenden ist, dann:
Nacheinander sollen beliebig viele Integer-Zahlen vom Benutzer eingegeben werden können.
Wird eine Null eingegeben, endet der Eingabeprozess und es wird die bis dahin größte Zahl mit Erklärtext ausgegeben.

#include<iostream>
using namespace std;
int main(void)
{
  int x;
  int y=-1;

  cout<<"Geben Sie beliebig viele positive Zahlen ein! 0 beendet das Programm und gibt den größten Wert aus."<<endl;
  do
  {
       cin>>x;
       if(x > y )
       {
              y=x;
       }     
  } while(x!=0);        
  cout<<"Der größte Wert ist "<< y <<endl;        
  return 0;
}

Code 0-10: Studentische Lösung.

Aufgabe 8.1.4

Schreiben Sie eine Java/Processing-Anwendung, bei der die Mausposition stets als Kreis dargestellt wird (Radius 15 Pixel).
Hinweis: Die aktuelle Mausposition ist durch die Variablen mouseX und mouseY verfügbar.

Schlagen Sie die Callback-Methode mouseClicked() in der Processing-Referenz nach.
Nutzen Sie diese Methode, um Positionen, an denen man klicked zu markieren.

int x=-100,y=-100;
public void setup()
{
     size(640,480);
}

public void draw()
{
     background(0,0,255);
     fill(255);
     ellipse(mouseX,mouseY,30,30);
     fill(255,0,0);
     ellipse(x,y,30,30);
}

public void mouseClicked()
{
     x=mouseX;
     y=mouseY;    
}

Code 0-11: Beispiellösung.

Aufgabe 8.1.5 -- spannende Sachen mit Java/Processing machen

Schauen Sie sich nach Start von Processing unter Datei -> Beispiele -> Basics -> Image den Sketch LoadDisplayImage an.
Testen Sie das Programm.
Speichern Sie eine Kopie dieses Sketches in Ihrem Sketchbook unter einem anderen Namen ab.
Variieren Sie das Programm in der Kopie.
Sie könnten beispielsweise die Bilder durch eigenen ersetzen, ein Bild hinzufügen, die Positionen ändern, oder sich dynamisch verändern lassen.

Verfahren Sie analog mit Datei -> Beispiele -> Libraries -> PDF Export -> OneFrame.
Sie könnten beispielsweise ein Poster erzeugen, oder ein Cover für eine CD.