Simulations- u. Regelungstechnik im Sommersemester 2025
(EN google-translate)
(PL google-translate)
|
 62_Regelungssysteme
62_Regelungssysteme
 54_Kinetik
54_Kinetik
 50_Simulationstechnik
50_Simulationstechnik
 37_Scilab
37_Scilab
 95_ETEST -- Hinweise zu der elektronischen Prüfungsform "E-Test"
95_ETEST -- Hinweise zu der elektronischen Prüfungsform "E-Test"
#1 Fr 28.03.2025
Motivation
Wir sind umgeben von komplexen dynamischen Systemen
 12_Technologie/03_Lottka_Volterra -- Lottka-Volterra-Modell (Räuber/Beute)
12_Technologie/03_Lottka_Volterra -- Lottka-Volterra-Modell (Räuber/Beute)
 12_Technologie/10_Start2019/04_Anthropozaen
12_Technologie/10_Start2019/04_Anthropozaen
Steuerungen
|
Geregelte technische Geräte und Komponenten
|
Was bedeutet Regelung im Vergleich zu Steuerung? -- Beispiele aus der Technik
 15_Einachser
15_Einachser
Autonomes Fahren Level 1 bis 5
Regelkreise in lebenden Systemen
|
Warum wird ein CAE-Tool (Computer added engineering) eingesetzt (Scilab)?
...und brandneu: Was bringt die Kombination mit ChatGPT?
Aufgabe für ChatGPT: Die Differentialgleichung dx/dt=x soll numerisch mit Hilfe des Euler-Integrationsverfahrens integriert werden. Es gelte: x(t=0s)=1. Es sollen 10 Integrationsschritte in einer Schrittweite von 0,1s durchgeführt werden. Damit wäre die Integrationszeit nach dem 10. Schritt bei 1,0 Sekunden. Schreiben Sie ein Scilab-Programm, das diese Aufgabe erledigt.
//Hier ist das Scilab-Programm, das die Differentialgleichung numerisch mit dem Euler-Integrationsverfahren löst:
// Set the initial condition
x0 = 1;
// Set the number of integration steps and the step size
n = 10;
dt = 0.1;
// Create arrays to store the time and solution values
t = 0:dt:dt*n;
x = zeros(1, n+1);
x(1) = x0;
// Perform the Euler integration
for i = 1:n
x(i+1) = x(i) + dt * x(i);
end
// Plot the results
plot(t, x)
xtitle('Numerical Solution of dx/dt = x', 'Time (s)', 'x')
//Das Programm gibt das Ergebnis als Grafik aus, die die numerische Lösung von x(t) gegen die Zeit t darstellt.
Code 0-1: Antwort von ChatGPT
Teil 1: Behandlung einführender Fragestellungen
|
 SYSTEM -- 50_Simulationstechnik/01_Systemtheorie/01_System
SYSTEM -- 50_Simulationstechnik/01_Systemtheorie/01_System
 MODELL -- 50_Simulationstechnik/01_Systemtheorie/02_Modell
MODELL -- 50_Simulationstechnik/01_Systemtheorie/02_Modell
Hinweis auf die besondere Bedeutung und Notwendigkeit der Visualisierung, wenn es um das Verstehen von Simulationsergebnissen geht.
 VERIFIKATION -- 50_Simulationstechnik/01_Systemtheorie/03_Verifikation
VERIFIKATION -- 50_Simulationstechnik/01_Systemtheorie/03_Verifikation
Teil 2: Einführung in Scilab
 Scilab, erste Schritte -- 37_Scilab/01_Erste_Schritte
Scilab, erste Schritte -- 37_Scilab/01_Erste_Schritte
 Scilab, Skripte -- 37_Scilab/02_Skripte
Scilab, Skripte -- 37_Scilab/02_Skripte
 Scilab, Funktionen -- 37_Scilab/03_Funktionen
Scilab, Funktionen -- 37_Scilab/03_Funktionen
Teil 3: Scilab und ein erstes Simulationsmodell
 Seerosenteich -- 50_Simulationstechnik/01_Systemtheorie/04_Seerosen
Seerosenteich -- 50_Simulationstechnik/01_Systemtheorie/04_Seerosen
 Euler-Integration -- 50_Simulationstechnik/01_Systemtheorie/05_Eulerintegration
Euler-Integration -- 50_Simulationstechnik/01_Systemtheorie/05_Eulerintegration
 Saalübung -- 50_Simulationstechnik/01_Systemtheorie/06_Saaluebung
Saalübung -- 50_Simulationstechnik/01_Systemtheorie/06_Saaluebung
 Umsetzung mit Scilab -- 50_Simulationstechnik/01_Systemtheorie/07_scilab
Umsetzung mit Scilab -- 50_Simulationstechnik/01_Systemtheorie/07_scilab
 62_Regelungssysteme/02_Heizregelkreis -- Der Regelkreis
62_Regelungssysteme/02_Heizregelkreis -- Der Regelkreis
ÜBUNGEN 28.03.2025
Übung mit Scilab
Aufgabe 1
Die Methode inv(...) ermöglicht es Matrizen zu invertieren und so lineare Gleichungssysteme zu lösen.
Beispielsweise kann folgendes LGS wie folgt mit Scilab gelöst werden:
$ \left[\begin{array}{cc}19 \\ 43\end{array}\right] = \left[\begin{array}{cc}1 & 2 \\ 3 & 4\end{array}\right] \cdot \left[\begin{array}{cc}x \\ y\end{array}\right] $
Formel 0-1: Lösung wäre: x=5 & y=7.
A=[1,2;3,4]; b=[19;43]; xy = inv(A)*b
Code 0-2: Lösung mit Hilfe von Scilab.
Lösen Sie folgende LGS mit Hilfe von Scilab:
$ \left[\begin{array}{cc}-26 \\ -12\end{array}\right] = \left[\begin{array}{cc}-1 & 2 \\ 3 & 4\end{array}\right] \cdot \left[\begin{array}{cc}x \\ y\end{array}\right] $
Formel 0-2: LGS2
$ \left[\begin{array}{cc}26 \\ 62 \\ 98\end{array}\right] = \left[\begin{array}{cc}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right] \cdot \left[\begin{array}{cc}x \\ y\end{array}\right] $
Formel 0-3: LGS2

Bild 0-1: Herleitung Feder-Masse-Schwinger (links), Euler-Integrationsverfahren (rechts).
Im Unterricht entstandenes Simulationsprogramm:
clear;
C=1; // N/M
m=1; // kg
x0=1; // m
v0=0; // m/s
dt=0.01; // s
t = 0;
x = x0;
v = v0;
x_merk = x0;
v_merk = v0;
t_merk = t;
n=1;
for t=0:dt:5
x_neu = x + v*dt;
v_neu = v + (-(C/m)*x)*dt;
x = x_neu;
v = v_neu;
n=n+1;
t=t+dt;
x_merk(1,n)=x;
v_merk(1,n)=v;
t_merk(1,n)=t;
end
plot(t_merk,x_merk,t_merk,v_merk);
Code 0-3: Feder-Masse-Schwinger mit Eulerintegrationsverfahren gelöst.
Aufgabe 2
|
Aufgabe 3
|
Musterlösung zu Aufgabe 3:
x0 = 1; dt=0.0001; x=x0; x_merk = x; t_merk = 0; n=1; for t=0:dt:5 x_neu = x + x*dt; x = x_neu; n=n+1; x_merk(1,n)=x; t_merk(1,n)=t; end y = exp(t_merk); plot(t_merk,x_merk,'red',t_merk,y,'blu--');
Code 0-4: Musterlösung zu Aufgabe 3.
#2 Fr 04.04.2025
Themen
|
1. Ergänzung eines linearen Dämpfers beim Feder-Masse-Schwinger
 54_Kinetik/01_Newton/02_Daempfung
54_Kinetik/01_Newton/02_Daempfung
2. Matrizendarstellung des linearen Differentialgleichungssystems erster Ordnung, das dem Feder-Masse-Dämpfer-System entspricht
 54_Kinetik/01_Newton/02_Daempfung
54_Kinetik/01_Newton/02_Daempfung
3. Einführung des numerischen Integrators ODE
 54_Kinetik/01_Newton/04_ODE
54_Kinetik/01_Newton/04_ODE
4. Eigenwertberechung für die Systemmatrix#h4
 50_Simulationstechnik/02_Eigenwerte/01_DGLS_Eigenwerte
50_Simulationstechnik/02_Eigenwerte/01_DGLS_Eigenwerte
5. Einführen einer externen Kraft zur Beruhigung (Ausregelung) des Feder-Masse-Schwingers
 Was ist ein Regelkreis? -- 62_Regelungssysteme/02_Heizregelkreis
Was ist ein Regelkreis? -- 62_Regelungssysteme/02_Heizregelkreis
6. Beschreibung eines Zustandsreglers
 62_Regelungssysteme/08_Polvorgabe
62_Regelungssysteme/08_Polvorgabe
7. Polvorgabe als Verfahren zur Auslegung eines Regelkreises
Tafelbilder
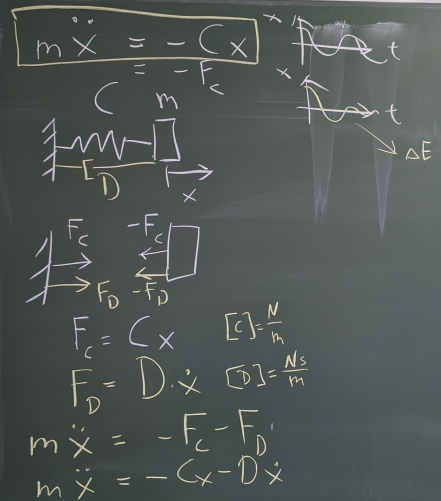
Bild 0-2: Lineares Feder-Masse-Dämpfer System.

Bild 0-3: Überführung des Systems in die Matrix-Darstellung.
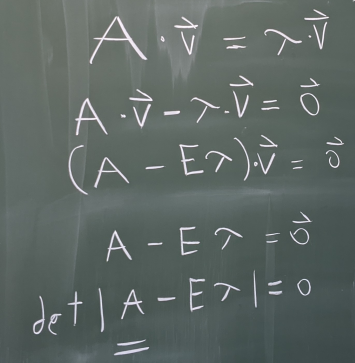
Bild 0-4: Wie werden Eigenwerte berechnet?
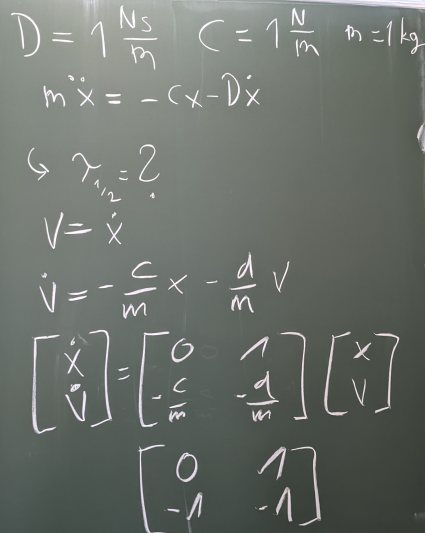
Bild 0-5: Bestimmung der Systemmatrix des Feder-Masse-Dämpfer Systems.

Bild 0-6: Bestimmung und Interpretation der Eigenwerte der Systemmatrix, hier: grenzstabil, da EW AUF der imaginären Achse. Hier: schwingungsfähig, da konjugiert komplexes Eigenwertpaar.
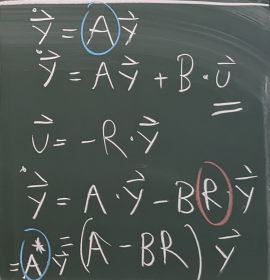
Bild 0-7: Das Konzept des Zustandsreglers: Die Eigenwerte werden durch (meistens negative) gewichtete (Matrix R) Rückkopplung der Systemzustände verschoben, es entsteht eine veränderte Systemmatrix A*.
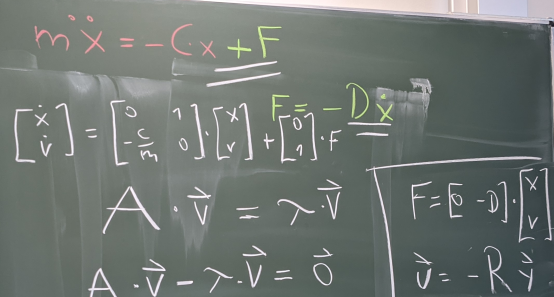
Bild 0-8: A* am Beispiel des Einbaus einer aktiven äußeren Kraft beim Feder-Masse-Schwinger.
8. Übungen
Aufgabe 1
Setzen Sie einen linearen Feder-Masse-Schwinger (ohne Dämpfung) um, der mit dem Euler-Verfahren in Scilab integriert wird. Es gelten folgende Eigenschaften: x0=0m, v0=1m/s, m=1 kg, C=4N/m.
Aufgabe 2
Bringen Sie das dynamische System aus Aufgabe 1 in Matrix-Darstellung
Aufgabe 3
Integrieren Sie das System aus Aufgabe 1 mittels des ODE-Integrators, anstatt mittels des selbst geschriebenen Euler-Integrators.
Aufgabe 4
Berechnen Sie die Eigenwerte des Systems aus Aufgabe 1. Überprüfen Sie Ihr Ergebnis mit der Scilab-Funktion spec(A).
Aufgabe 5
Führen Sie eine Aktive Kraft F = -D*v in das System ein, mit D=1Ns/m. Stellen Sie die Gleichungen dieses Systems auf.
Aufgabe 6
Berechnen Sie die veränderten Eigenwerte, die sich nun bei dem System von Aufgabe 5 ergeben. Überprüfen Sie Ihr Ergebnis mit der Scilab-Funktion spec(A).
#3 Fr 11.04.2025
Themen
|
1. Wiederholung der Theorie von letzter Woche: Eigenwerte, Systemmatrix, Zustandsregler
2. Ergänzung der Newton-Gleichung durch die Euler-Gleichung
 Newton-Eulersche Gleichungen -- 54_Kinetik/02_NewtonEuler
Newton-Eulersche Gleichungen -- 54_Kinetik/02_NewtonEuler
 Hauptträgheitsmomente von einfachen Körpern -- 54_Kinetik/02_NewtonEuler/01_Traegheitsmomente
Hauptträgheitsmomente von einfachen Körpern -- 54_Kinetik/02_NewtonEuler/01_Traegheitsmomente
 Aufstellen der Modellgleichungen für Mehrkörpersysteme -- 54_Kinetik/02_NewtonEuler/02_Modellgleichungen
Aufstellen der Modellgleichungen für Mehrkörpersysteme -- 54_Kinetik/02_NewtonEuler/02_Modellgleichungen
 Einfachpendel -- 54_Kinetik/02_NewtonEuler/03_Einfachpendel
Einfachpendel -- 54_Kinetik/02_NewtonEuler/03_Einfachpendel
3. Einführung eines komplexeren Beispiels: das invertierte Pendel
|
 62_Regelungssysteme/16_Inverses_Pendel
62_Regelungssysteme/16_Inverses_Pendel
 Tafelbilder 0-4 und 0-5: 62_Regelungssysteme/01_day_by_day
Tafelbilder 0-4 und 0-5: 62_Regelungssysteme/01_day_by_day
4. Übungen
|
WIEDERHOLUNG und erste Auslegung eines Zustandsreglers
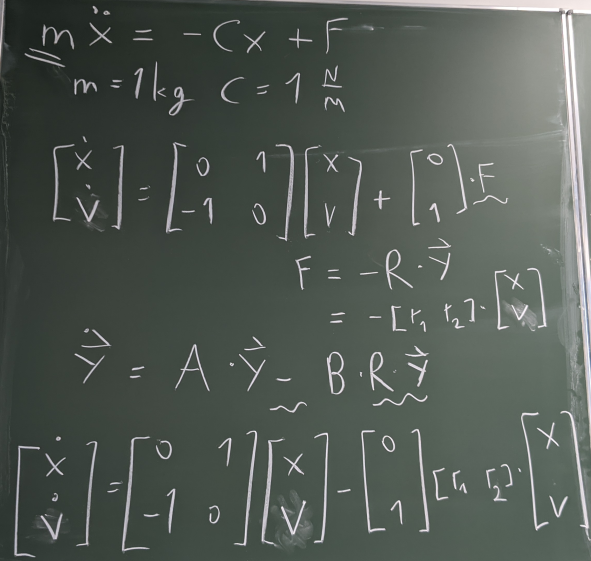
Bild 0-9: Auslegung eines Zustandsreglers für das grenzstabile System des linearen Feder-Masse-Schwingers.
![Festlegung der Wunscheigenwerte (hier -1+i und -1-i) und Bestimmung von R=[r1 r2] durch Koeffizientenvergleich.](http://www.kramann.info/02_SoSe2025/01_SRT_day_by_day/z2.png)
Bild 0-10: Festlegung der Wunscheigenwerte (hier -1+i und -1-i) und Bestimmung von R=[r1 r2] durch Koeffizientenvergleich.
Herleitung der Simulationsgleichung des Körperpendels

Bild 0-11: Aufstellen der Newton-Euler-Gleichungen und Bestimmung des durch die Zwangskräfte Fx und Fy hervorgerufenen Moments.
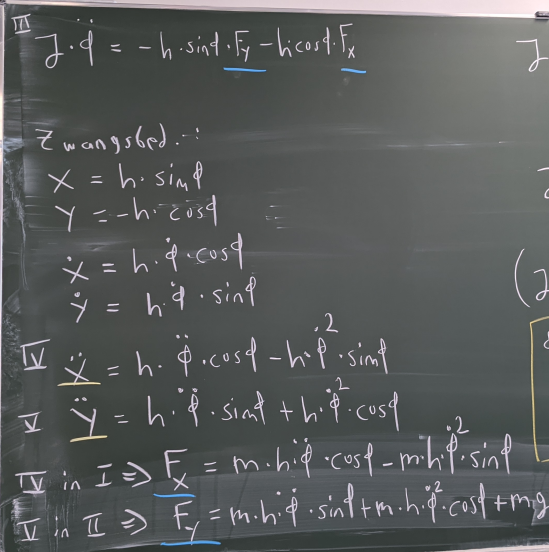
Bild 0-12: Ausnutzung der Zwangsbedingungen durch zweimalige Ableitung, dann in die Newton-Gleichungen einsetzen, um Fx und Fy in Abhängigkeit von phi, phi_punkt und Phi_zweipunkt zu bestimmen.
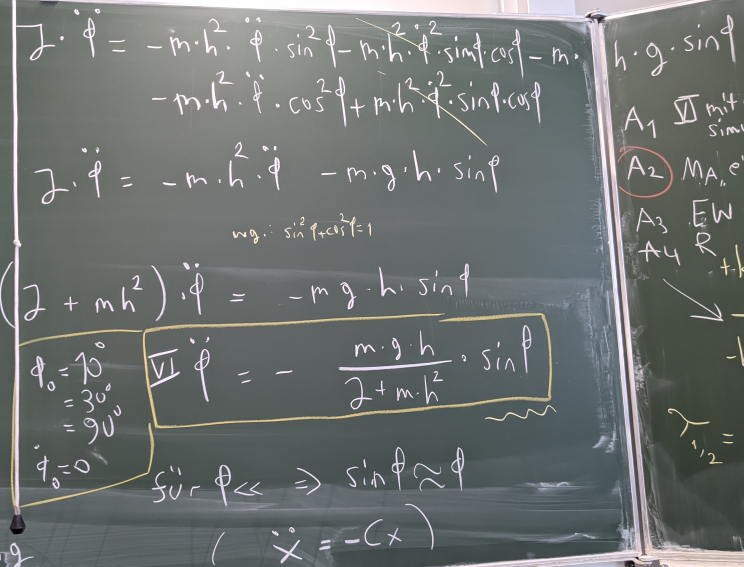
Bild 0-13: Einsetzen von Fx und Fy in die Euler-Gleichung, um die Unbekannten dort zu eliminieren. Dann Zusammenfassen der Terme.
ÜBUNGSAUFGABEN auf Grundlage des Körperpendels:
Aufgabe1: Simulieren Sie die resultierende dynamische Euler-Gleichung mit ODE in Scilab. Verwenden Sie folgende Parameter: l=1m (h=0,5m) m=1kg r=0,1m phi_null = 10 Grad, 30 Grad, 90 Grad (als Tests), phi_punkt_null=0 rad/s Aufgabe2: Ein Antriebsmoment MA zusätzlich in die dynamischen Gleichungen des Körperpendels einbauen und die gesamte Herleitung damit nochmal anpassen, bis man wieder die Eulergleichung ohne Unbekannte hat. Aufgabe3: Bestimmen Sie die Eigenwerte der linearisierten dynamischen Gleichungen des Körperpendels. Aufgabe4: Legen Sie einen Zustandsregler für das linearisierte System des Körperpendels so aus, dass wenn k der Betrag bei dem ursprünglich konjugiert komplexen Eigenwertpaar auf der imaginären Achse ist,
Code 0-5: dann die Wunscheigenwerte bei -k+k*i und -k-k*i liegen.
clear;
m=1;
l=1;
h=l/2;
r=1.1;
g=9.81;
J=0.25*m*r*r + (1/12)*m*l*l;
Q=(m*g*h)/(J+m*h*h);
function f = rechteSeite(t,y)
phi = y(1,1);
w = y(2,1);
f(1,1) = w;
f(2,1) = -Q*sin(phi);
endfunction
t = 0:0.01:15;
y0 = [170*%pi/180,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-6: Lösung zu Aufgabe 1.

Bild 0-14: Plot zu Lösung zu Aufgabe 1.
clear;
m=1;
l=1;
h=l/2;
r=1.1;
g=9.81;
J=0.25*m*r*r + (1/12)*m*l*l;
Q=(m*g*h)/(J+m*h*h);
//Zustandsregler auslegen:
A = [0,1;-Q,0]
EW = spec(A)
K = abs(EW(1))
EWwunsch = [-K+%i*K,-K-%i*K]
B=[0;1/(J+m*h*h)]
R=ppol(A,B,EWwunsch)
//Simulation des geregelten Systems:
function f = rechteSeite(t,y)
phi = y(1,1);
w = y(2,1);
MA = R(1)*phi + R(2)*w;
f(1,1) = w;
f(2,1) = -Q*sin(phi) - (1/(J+m*h*h))*MA;
endfunction
t = 0:0.01:15;
y0 = [170*%pi/180,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)',t,y(2,:)');
Code 0-7: Lösung zu Aufgabe 4 nur in Scilab.

Bild 0-15: Plot zu Lösung zu Aufgabe 4.
4. Übungen (VERWORFEN)
Aufgabe 1
|
Aufgabe 2
|
Vorschau: Nächstes mal: Linearisierung des invertierten Pendels und Einbau und Auslegung eines Zustandsreglers.
#4 Fr 25.04.2025
Themen
|
1. Beginn mit der Theorie zu Optimierungsverfahren
 50_Simulationstechnik/06_Optimierung
50_Simulationstechnik/06_Optimierung
2. Koordinatentransformationen im R2
 54_Kinetik/03_Kinematik/01_Koordinatentransformation
54_Kinetik/03_Kinematik/01_Koordinatentransformation

Bild 0-16: Koordinatentransformation bei einer rein translatorischen Verschiebung.

Bild 0-17: Rotierte Koordinaten als Linearkombination der orthogonalen Einheitsvektoren des rotierten Koordinatensystems, dargestellt im Inertialkoordinatensystem.
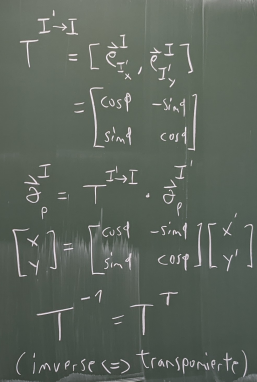
Bild 0-18: Zusammenfassung der Einheitsvektoren zu einer Transformationsmatrix.

Bild 0-19: Vorgehensweise, wenn Translation und Rotation miteinander kombiniert sind.
3. Herleitung der Simulationsgleichungen zum invertierenden Pendel
 62_Regelungssysteme/01_day_by_day -- alte Herleitung zur Orientierung, siehe "9 -- Dienstag 21.05.2019 "
62_Regelungssysteme/01_day_by_day -- alte Herleitung zur Orientierung, siehe "9 -- Dienstag 21.05.2019 "

Bild 0-20: Aufstellen der Newton-Euler-Gleichungen.
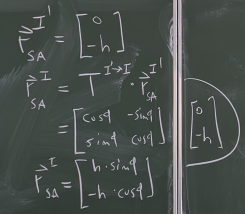
Bild 0-21: Bestimmung des Verbindungsvektors von Punkt S zu Punkt A unter Ausnutzung der zuvor gewonnenen rotatorischen Transformationsmatrix.
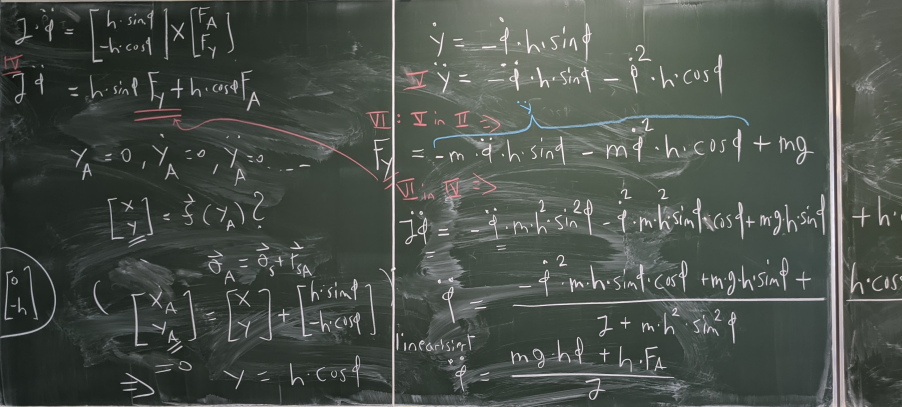
Bild 0-22: Elimination von Fy unter Ausnutzung der Zwangsbedingungen.
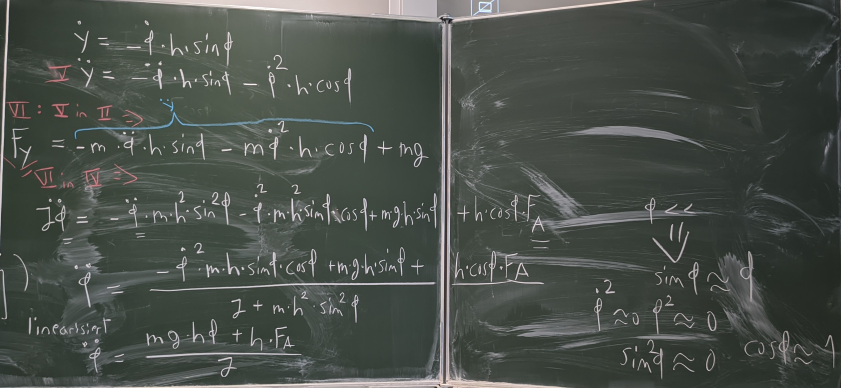
Bild 0-23: Linearisierung der Simulationsgleichung.
4. Linearisierung der dynamischen Gleichungen des invertierenden Pendels
5. ÜBUNG Auslegung eines Zustandsreglers für das invertierende Pendel
|
clear;
m = 1;
l = 1;
h = 1/2;
r = 0,1;
g = 9.81;
J = 1/4*m*r^2+1/12*m*l^2;
Q = (m*g*h)/J;
A = [0,1; Q,0];
B = [0; h/J];
EW = spec(A);
k = abs(EW(1));
P = [-k+k*%i;-k-k*%i];
R = ppol(A,B,P);
function f = rechts(t,y)
phi = y(1,1);
w = y(2,1);
F_a = -R*y;
f(1,1) = w
f(2,1) = Q*phi+(h/J)*F_a;
endfunction
t = 0:0.01:2;
y0 = [0.1;0];
t0 = 0;
y = ode(y0,t0,t,rechts);
plot(t,y(1,:)',t,y(2,:)');
Code 0-8: Studentische Lösung, Teil 1. bis 5.
#5 Fr 02.05.2025
Themen
|
Vorbetrachtungen: Zusamenschau der Systemgleichungen:
$ \ddot \phi = \frac {-\dot \phi ^2 \cdot m \cdot h \cdot \sin \left( \phi \right) \cdot \cos \left( \phi \right)+m \cdot g \cdot h \cdot \sin \left( \phi \right)+h \cdot \cos \left( \phi \right) \cdot F_A}{J+m \cdot h^2 \cdot \sin ^2\left( \phi \right) } $
Formel 0-4: Eulergleichung des nicht linearisierten invertierenden Pendels.
$ \ddot \phi = \frac {m \cdot g \cdot h \cdot \phi +h \cdot F_A}{J} $
Formel 0-5: Linearisierte Fassung der Eulergleichung des invertierenden Pendels.
$ \left[\begin{array}{cc}\dot \phi \\ \dot \omega \end{array}\right]=\left[\begin{array}{cc}0 & 1 \\ \frac {m \cdot g \cdot h}{J} & 0\end{array}\right] \cdot \left[\begin{array}{cc} \phi \\ \omega \end{array}\right]+\left[\begin{array}{cc}0 \\ \frac {h}{J}\end{array}\right] \cdot F_A $
Formel 0-6: Linearisierte Fassung der Eulergleichung des invertierenden Pendels in Matrix-Schreibweise.
$ \dot \vec y = A \cdot \vec y + B \cdot \vec u $
Formel 0-7: Allgemeine Darstellung der Matrix-Schreibweise.
R = ppol(A,B,EW)
Code 0-9: Verwendung von ppol zur Auslegung eines Zustandsreglers unter Vorgabe der Wunscheigenwerte für A* durch EW.
$ \vec u = -R \cdot \vec y $
Formel 0-8: Beim Zus \tan dsregler werden die Zustände mit Linearfaktoren gewichtet auf das System negativ zurück geführt.
$ \dot \vec y = A \cdot \vec y - B \cdot R \cdot \vec y $
Formel 0-9: Zus \tan ds-geregeltes System allgemein.
$ Astern = A - B \cdot R $
Formel 0-10: Allgemeine Darstellung des Zusammenhangs zwischen Astern und A.
$ \left[\begin{array}{cc}\dot \phi \\ \dot \omega \end{array}\right]=\left[\begin{array}{cc}0 & 1 \\ \frac {m \cdot g \cdot h}{J} & 0\end{array}\right] \cdot \left[\begin{array}{cc} \phi \\ \omega \end{array}\right]-\left[\begin{array}{cc}0 \\ \frac {h}{J}\end{array}\right] \cdot \left[\begin{array}{cc}r_1 r_2\end{array}\right] \cdot \left[\begin{array}{cc} \phi \\ \omega \end{array}\right] $
Formel 0-11: Zus \tan ds-geregeltes linearisiertes System beim invertierenden Pendel.
$ F_A = -r_1 \cdot \phi - r_2 \cdot \omega $
Formel 0-12: Bestimmung der Antriebskraft FA beim Zus \tan ds-geregelten System.
1. Verifikation der Brauchbarkeit des Zustandsreglers durch Einbau in das nicht linearisierte Modell
2. Ausregelung aller Zustandsgrößen, also sowohl phi, als auch x beim invertierenden Pendel
 Einachser Hardware mit Arduino Micro und IMU MPU6050: http://www.kramann.info/___downloads/einachser3.ogg
Einachser Hardware mit Arduino Micro und IMU MPU6050: http://www.kramann.info/___downloads/einachser3.ogg
 Siehe auch "Musterlösung zu Übung 2 vom 15.12.2020 " hier: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21 (Fallback)
Siehe auch "Musterlösung zu Übung 2 vom 15.12.2020 " hier: 62_Regelungssysteme/98_day_by_day_WS2021_SoSe21 (Fallback)
ÜBUNG
|
$ \left[\begin{array}{cc}\dot x \\ \dot v \\ \dot \phi \\ \dot \omega \end{array}\right] = \left[\begin{array}{cc}0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac {m \cdot g \cdot h}{J} & 0\end{array}\right] \cdot \left[\begin{array}{cc}x \\ v \\ \phi \\ \omega \end{array}\right]+\left[\begin{array}{cc}0 \\ \frac {1}{m} \\ 0 \\ \frac {h}{J}\end{array}\right] \cdot F_A $
Formel 0-13: Linearisiertes DGLS in Matrixform.
clear;
m = 1;
l = 1;
h = 1/2;
r = 0.1;
g = 9.81;
J = 1/4*m*r^2+1/12*m*l^2;
Q = (m*g*h)/J;
A = [0,1,0,0; 0,0,0,0; 0,0,0,1; 0,0,Q,0];
B = [0; 1/m; 0; h/J];
EW = spec(A);
k = abs(EW(1));
P = [-k+k*%i; -k-k*%i;-2*k+k*%i; -2*k-k*%i];
R = ppol(A,B,P);
function f = rechts(t,y)
x = y(1,1);
v = y(2,1);
phi = y(3,1);
w = y(4,1);
F_a = -R*y;
sp = sin(phi);
cp = cos(phi);
f(1,1) = v;
f(2,1) = (1/m)*F_a;
f(3,1) = w;
//f(4,1) = Q*phi+(h/J)*F_a; //Lineare Variante
f(4,1) = (-w^2*m*h^2*sp*cp+m*g*h*sp+h*cp*F_a)/(J+m*h^2*sp^2);
endfunction
//Verwendung der Matrixform (nur für linearisierte Variante möglich):
//function dx=rechts(t, x)
// u = -R*x;
// dx = A*x + B*u;
//endfunction
t = 0:0.01:1;
y0 = [0.1; 0; 0.1; 0];
t0 = 0;
y = ode(y0,t0,t,rechts);
plot(t,y(1,:)',"r", t,y(2,:)',"b", t,y(3,:)',"g", t,y(4,:)',"m");
Code 0-10: Studentische Lösung(en)
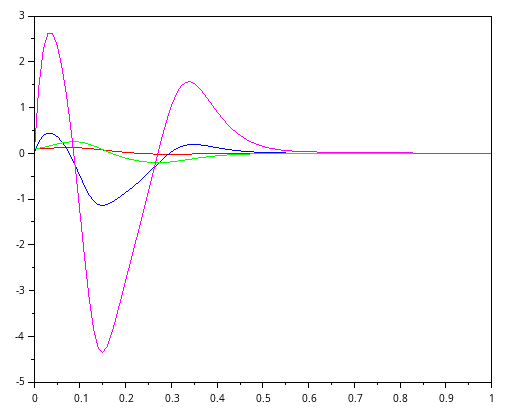
Bild 0-24: Ausregeln vierer Systemzustände für den nicht linearen Fall.
3. Zustandsregler für Systeme, die nicht zu Null ausgeregelt werden
 Modell eines Gleichstrommotors -- 62_Regelungssysteme/05_Regleroptimierung/06_Gleichstrommotor
Modell eines Gleichstrommotors -- 62_Regelungssysteme/05_Regleroptimierung/06_Gleichstrommotor
 Polvorgabe für den Gleichstrommotor -- 62_Regelungssysteme/08_Polvorgabe
Polvorgabe für den Gleichstrommotor -- 62_Regelungssysteme/08_Polvorgabe
ÜBUNG
|
4. Entwurf modifiziertes Gradientenverfahren für das nicht linearisierte Modell des invertierenden Pendels
 Scilab-Syntax-Unterstützung, siehe auch: "Code 0-9: optimierer.sce " hier: 62_Regelungssysteme/01_day_by_day
Scilab-Syntax-Unterstützung, siehe auch: "Code 0-9: optimierer.sce " hier: 62_Regelungssysteme/01_day_by_day
################################
SNIPPET Zufallswerte in Scilab:
dx = floor(grand(1, 1, "unf", 0, 2.999999999)) - 1; //liefert -1 oder +1 zufällig
################################
MODELL.SCE:
R1=10.153333;
R2=0.3433333;
m = 1; //kg
g = 9.81; //m/s^2
h = 0.5; //m
r = 0.1; //m
l = 2*h; //m
J = 0.25*m*r^2 + (1/12)*m*l; // kg*m^2
function f = rechteSeite(t,y)
phi = y(1,1);
om = y(2,1);
f(1,1) = om;
FA = -R1*phi -R2*om;
N = J + m*h*h*sin(phi)*sin(phi);
f(2,1) = (-m*h*h*om*om*sin(phi)*cos(phi) + h*m*sin(phi)*g + h*cos(phi)*FA )/N;
endfunction
################################
FEHLERFUNKTION.SCE
function z = berechneFehler(RR1,RR2)
R1 = RR1;
R2 = RR2;
t = linspace(0,20,3000);
y0 = [0.2,0.1]';
t0 = 0;
yy = ode(y0,t0,t,rechteSeite);
fehler = sum(abs(yy(1,:)));
z = fehler;
endfunction
################################
OPTIMIERER.SCE
clear();
exec modell.sce
exec fehlerfunktion.sce
################################
SNIPPET ZUR ANIMATION
x = y(3,:);
phi = y(1,:);
y = h.*cos(phi);
zs = size(t);
spalten = zs(2);
pA = [x + h.*sin(phi);zeros(1,spalten)];
pB = [x - h.*sin(phi);y + h.*cos(phi)];
//Eine Animation soll eine Verbindungslinie von pA mit pB im zeitlichen Verlauf darstellen:
isoview;
clf;
// ABBRUCH MIT CTR C !!
for i=1:spalten
clf;
plot([-1.2,-1.1999,1.1999,1.2],[-1.2,1.2,1.2,-1.2]); //Rahmen, um Skalierung konstant zu halten
plot([pA(1,i),pB(1,i)],[pA(2,i),pB(2,i)]);
sleep(10); // "Echtzeit"
end
Code 0-11: ...insbesondere die Programmstruktur in Scilab.
#5 Fr 02.05.2025
Themen
|
1. Wie ist ein Regelkreis aufgebaut?
 62_Regelungssysteme/02_Heizregelkreis
62_Regelungssysteme/02_Heizregelkreis
2. Verzögerungsglieder
 62_Regelungssysteme/03_Verzoegerungsglieder
62_Regelungssysteme/03_Verzoegerungsglieder
3. Einführung in die Laplace Transformation
 62_Regelungssysteme/04_Laplace
62_Regelungssysteme/04_Laplace
 62_Regelungssysteme/04_Laplace/03_PRegler
62_Regelungssysteme/04_Laplace/03_PRegler
//s als Argument für ein Polynom definieren:
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[1+2*s+s^2]);
t=[0:0.01:10];
u=ones(1,1001);
y=csim(u,t,G);
plot2d(t,y);
//plzr(G);
Code 0-12: Verwendung von Scilab zur Handhabung von Übertragungsfunktionen (Beispiel).
Vergleich: Feder-Masse-Schwinger mit Scilab im Zeitbereich und im Laplace-Bereich beschreiben und simulieren
m = 1.0;
C = 1.0;
D = 1.0;
F = 10.0;
function f = rechteSeite(t,y)
x = y(1,1);
v = y(2,1);
f(1,1) = v;
f(2,1) = -(C/m)*x -(D/m)*v + F/m;
endfunction
t = linspace(0,30,3000);
y0 = [0,0]';
t0 = 0;
y = ode(y0,t0,t,rechteSeite);
plot(t,y(1,:)','gre');
// -----------------------------------------
// Laplace-Darstellung:
//s als Argument für ein Polynom definieren:
s = poly(0,"s");
//Übertragungsfunktion definieren:
G = syslin('c',[1],[m*s*s + D*s + C]);
u=10*ones(1,3000); //entspricht F
y=csim(u,t,G);
plot(t,y,'blu--');
//plzr(G);
Code 0-13: Feder-Masse-Schwinger mit äußerer Kraft F im Zeit- und Laplacebereich simulieren.
4. ÜBUNG 1 zu Laplace-Transformation mit Scilab
Eigenwerte können auch über Nullstellen des Nenners einer Übertragungsfunktion bestimmt werden.
|
Zweiter Teil der ersten Übung:
|
$ \ddot x+3 \cdot x=4 \cdot u $
Formel 0-14: a
$ \dot x-x=u $
Formel 0-15: b
$ 3 \ddot x+\dot x=u $
Formel 0-16: c
$ \ddot x+x=u $
Formel 0-17: d
$ \dot x+2 \cdot x=u $
Formel 0-18: e
$ \dot x-3 \cdot x=u $
Formel 0-19: f
$ \dot x+5 \cdot x=5 \cdot u $
Formel 0-20: g
5. ÜBUNG 2 zu Laplace-Transformation mit Scilab
Plotten Sie mit Scilab für folgende Systeme den Einheitssprung. Führen Sie dazu die notwendige Laplace-Transformation aus und finden Sie selber eine sinnvolle Simulationsdauer:
$ \ddot x + \dot x + 3 x = 4 u $
Formel 0-21: a
$ 3 \ddot x + \dot x = u $
Formel 0-22: b
$ \ddot x + x = u $
Formel 0-23: c
$ \dot x + 2 x = u $
Formel 0-24: d
$ \dot x - x = u $
Formel 0-25: e
#6 Fr 16.05.2025
Themen
Nachbesprechung Übung 2b letzte Woche Verkettung zwei PT1 Laplace / Zeitbereich Regeln Laplace P-Regler Laplace / Zeitbereich ÜBUNG: PD-Regler Totzeitglied Runge-Kutta-Integrator Methode 1 nach Ziegler und Nichols
Code 0-14: Themen
 62_Regelungssysteme/07_Einstellregeln
62_Regelungssysteme/07_Einstellregeln
 62_Regelungssysteme/07_Einstellregeln/02_Methode1
62_Regelungssysteme/07_Einstellregeln/02_Methode1
clear(); xtot=0; function f=modell(y,t,dt) x=y(1,1); v=y(2,1); Kkrit = 19.75; xsoll = 1.0; //e = xsoll - x; e = xsoll - xtot; u=Kkrit*e; f(1,1)=v; f(2,1)=-x-2*v+u; endfunction function yneu=ruku(y,t,dt) k1=modell(y,t,dt); k2=modell(y+0.5.*dt.*k1,t+0.5*dt); k3=modell(y+0.5.*dt.*k2,t+0.5*dt); k4=modell(y+dt.*k3,t+dt); yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6; endfunction tmax = 20.0; dt = 0.01; schritte = ceil(tmax/dt); yalt = [0,0]'; ysim = yalt; t=0.0; tt=t; Ttot = 0.1; anztot = round(Ttot/dt) xtotarr = zeros(anztot,1); for i=1:1:schritte yneu=ruku(yalt,t,dt); yalt=yneu; ysim=[ysim,yalt]; tt =[tt,t]; t=t+dt; xtot = xtotarr(modulo((i-1),anztot)+1); xtotarr(modulo((i-1),anztot)+1)=yneu(1); end plot(tt,ysim(1,:));
Code 0-15: Beispielcode Methode 1 Ziegler / Nichols.
 30_Informatik3/16_Nuetzliches/03_RungeKutta -- Runge-Kutta-Integrator.
30_Informatik3/16_Nuetzliches/03_RungeKutta -- Runge-Kutta-Integrator.
ÜBUNG
|
#7 Fr 23.05.2025
Themen
|
1. Quiz -- Wiederholung des Unterrichtsstoffes
2. Behandlung des Integralanteils beim PI, bzw. beim PID-Regler im Laplace- und im Zeitbereich
clear(); xtot=0; function f=modell(y,t,dt) x=y(1,1); v=y(2,1); eI=y(3,1); //Integral der Regeldifferenz Kkrit = 19.75; Tkrit = 1.45; //PI-Regler: K=0.45*Kkrit; TN=0.85*Tkrit; xsoll = 1.0; //e = xsoll - x; e = xsoll - xtot; //u=Kkrit*e; u=K*e + (K/TN)*eI; f(1,1)=v; f(2,1)=-x-2*v+u; f(3,1)=e; endfunction function yneu=ruku(y,t,dt) k1=modell(y,t,dt); k2=modell(y+0.5.*dt.*k1,t+0.5*dt); k3=modell(y+0.5.*dt.*k2,t+0.5*dt); k4=modell(y+dt.*k3,t+dt); yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6; endfunction tmax = 20.0; dt = 0.01; schritte = ceil(tmax/dt); yalt = [0,0,0]'; //jetzt dritter Startwert eI0=0 ysim = yalt; t=0.0; tt=t; Ttot = 0.1; anztot = round(Ttot/dt) xtotarr = zeros(anztot,1); for i=1:1:schritte yneu=ruku(yalt,t,dt); yalt=yneu; ysim=[ysim,yalt]; tt =[tt,t]; t=t+dt; xtot = xtotarr(modulo((i-1),anztot)+1); xtotarr(modulo((i-1),anztot)+1)=yneu(1); end plot(tt,ysim(1,:));
Code 0-16: Ergänzen des I-Anteils und Simulation mit eingebautem PI-Regler, der Mit Ziegler-Nichols ausgelegt wurde.
3. Besprechung der Übung von letzter Woche zum Einstellregler nach Ziegler und Nichols, insbesondere Auslegung P-, PI- und PID-Regler.
4. ÜBUNG (Einstellregler nach Ziegler und Nichols)
|
Kkrit finden
clear(); xtot=0; function f=modell(y,t,dt) x=y(1,1); v=y(2,1); Kkrit = 0.49; Tkrit = 8.125; C=0.1; D=0.1; //PI-Regler: K=0.45*Kkrit; I=0.85*Tkrit; xsoll = 2.0; //e = xsoll - x; e = xsoll - xtot; u=Kkrit*e; f(1,1)=v; f(2,1)=-C*x-D*v+u; endfunction function yneu=ruku(y,t,dt) k1=modell(y,t,dt); k2=modell(y+0.5.*dt.*k1,t+0.5*dt); k3=modell(y+0.5.*dt.*k2,t+0.5*dt); k4=modell(y+dt.*k3,t+dt); yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6; endfunction tmax = 80.0; dt = 0.01; schritte = ceil(tmax/dt); yalt = [0,0]'; ysim = yalt; t=0.0; tt=t; Ttot = 0.2; anztot = round(Ttot/dt) xtotarr = zeros(anztot,1); for i=1:1:schritte yneu=ruku(yalt,t,dt); yalt=yneu; ysim=[ysim,yalt]; tt =[tt,t]; t=t+dt; xtot = xtotarr(modulo((i-1),anztot)+1); xtotarr(modulo((i-1),anztot)+1)=yneu(1); end plot(tt,ysim(1,:));
Code 0-17: Ziegler-Nichols, Kkrit finden.
PI-Regler nach Ziegler-Nichols.
clear(); xtot=0; function f=modell(y,t,dt) x=y(1,1); v=y(2,1); eI=y(3,1); //Integral der Regeldifferenz Kkrit = 0.49; Tkrit = 8.125; C=0.1; D=0.1; //PI-Regler: K=0.45*Kkrit; TN=0.85*Tkrit; xsoll = 2.0; //e = xsoll - x; e = xsoll - xtot; //u=0.5*Kkrit*e; u=K*e + 0.1*(K/TN)*eI; f(1,1)=v; f(2,1)=-C*x-D*v+u; f(3,1)=e; endfunction function yneu=ruku(y,t,dt) k1=modell(y,t,dt); k2=modell(y+0.5.*dt.*k1,t+0.5*dt); k3=modell(y+0.5.*dt.*k2,t+0.5*dt); k4=modell(y+dt.*k3,t+dt); yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6; endfunction tmax = 200.0; dt = 0.01; schritte = ceil(tmax/dt); yalt = [0,0,0]'; //jetzt dritter Startwert eI0=0 ysim = yalt; t=0.0; tt=t; Ttot = 0.2; anztot = round(Ttot/dt) xtotarr = zeros(anztot,1); for i=1:1:schritte yneu=ruku(yalt,t,dt); yalt=yneu; ysim=[ysim,yalt]; tt =[tt,t]; t=t+dt; xtot = xtotarr(modulo((i-1),anztot)+1); xtotarr(modulo((i-1),anztot)+1)=yneu(1); end plot(tt,ysim(1,:));
Code 0-18: Ziegler-Nichols, PI-Regler testen.
PID-Regler nach Ziegler-Nichols
clear(); xtot=0; function f=modell(y,t,dt) x=y(1,1); v=y(2,1); eI=y(3,1); //Integral der Regeldifferenz Kkrit = 0.49; Tkrit = 8.125; C=0.1; D=0.1; //PID-Regler: K=0.6*Kkrit; TN=0.5*Tkrit; TV=0.12*Tkrit; xsoll = 2.0; //e = xsoll - x; e = xsoll - xtot; //u=0.5*Kkrit*e; u=K*e + (K/TN)*eI - TV*v; f(1,1)=v; f(2,1)=-C*x-D*v+u; f(3,1)=e; endfunction function yneu=ruku(y,t,dt) k1=modell(y,t,dt); k2=modell(y+0.5.*dt.*k1,t+0.5*dt); k3=modell(y+0.5.*dt.*k2,t+0.5*dt); k4=modell(y+dt.*k3,t+dt); yneu=y+dt.*(k1+2.*k2+2.*k3+k4)./6; endfunction tmax = 200.0; dt = 0.01; schritte = ceil(tmax/dt); yalt = [0,0,0]'; //jetzt dritter Startwert eI0=0 ysim = yalt; t=0.0; tt=t; Ttot = 0.2; anztot = round(Ttot/dt) xtotarr = zeros(anztot,1); for i=1:1:schritte yneu=ruku(yalt,t,dt); yalt=yneu; ysim=[ysim,yalt]; tt =[tt,t]; t=t+dt; xtot = xtotarr(modulo((i-1),anztot)+1); xtotarr(modulo((i-1),anztot)+1)=yneu(1); end plot(tt,ysim(1,:));
Code 0-19: Ziegler-Nichols, PID-Regler testen.
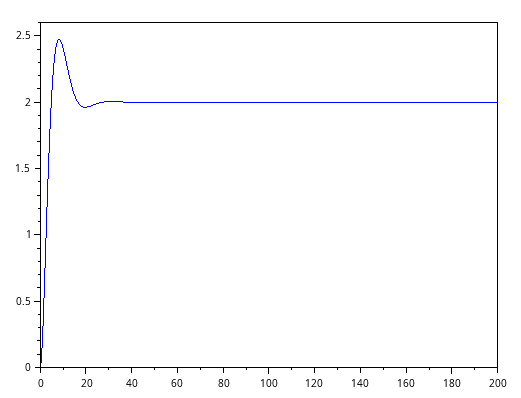
Bild 0-25: Plot zum System mit PID-Regler.
Prüfen der Eigenwertlagen
//s als Argument für ein Polynom definieren:
s = poly(0,"s");
//Übertragungsfunktion definieren:
C=0.1;
D=0.1;
Kkrit = 0.49;
Tkrit = 8.125;
C=0.1;
D=0.1;
//PID-Regler:
K=0.6*Kkrit;
TN=0.5*Tkrit;
TV=0.12*Tkrit;
//K=0.45*Kkrit;
//TN=0.85*Tkrit;
G = syslin('c',[1],[s*s+C*s+D]);
R = syslin('c',[K*TN*TV*s*s+K*TN*s+K],[TN*s]);
H=G*R;
Q=H/(H+1);
t = linspace(0,30,3000);
u=2*ones(1,3000); //entspricht F
y=csim(u,t,Q);
//plot(t,y,'blu--');
plzr(Q);
Code 0-20: Prüfen der Eigenwertlagen.
#8 Fr 06.06.2025
Themen
Heute werden wir einige Ergänzungen zur Theorie der Regelungstechnik vornehmen, die insgesamt mehr Sicherheit im Umgang mit Regelstrecken vermitteln werden.
|
1. Stabilität einer Übertragungsfunktion
 siehe: 62_Regelungssysteme/11_Stabilitaet
siehe: 62_Regelungssysteme/11_Stabilitaet
Kurzfassung: Zählergrad <= Nennergrad UND EW in linker Halbebene.
2. Experimentelle Ansätze (statische und dynamische Stabilität):
 Untersuchungen zu dynamischer Stabilität: 62_Regelungssysteme/11_Stabilitaet/01_Beispiele
Untersuchungen zu dynamischer Stabilität: 62_Regelungssysteme/11_Stabilitaet/01_Beispiele
3. Das Nyquistkriterium
 62_Regelungssysteme/11_Stabilitaet/02_Nyqusitkriterium
62_Regelungssysteme/11_Stabilitaet/02_Nyqusitkriterium
ÜBUNG
 Siehe unten bei "Aufgaben" hier: 62_Regelungssysteme/11_Stabilitaet/02_Nyqusitkriterium
Siehe unten bei "Aufgaben" hier: 62_Regelungssysteme/11_Stabilitaet/02_Nyqusitkriterium
4. Windup und Anti-Windup
 siehe: 62_Regelungssysteme/11_Stabilitaet/03_Windup
siehe: 62_Regelungssysteme/11_Stabilitaet/03_Windup
5. Regelbarkeit, Führungsverhalten und Störverhalten
 siehe: 62_Regelungssysteme/13_Analyse/01_Linear
siehe: 62_Regelungssysteme/13_Analyse/01_Linear
Regelungen sind überhaupt nur notwendig, weil Systeme im Allgemeinen vielfältigen Störeinflüssen unterliegen, so, dass eine Steuerung nicht zielführend wäre.
Störung können beispielsweise sein:
|
|
ÜBUNG
|
 siehe weiter unten bei "Störverhalten" hier: 62_Regelungssysteme/13_Analyse/01_Linear
siehe weiter unten bei "Störverhalten" hier: 62_Regelungssysteme/13_Analyse/01_Linear
6. Beurteilung nicht linearer Systeme
 siehe: 62_Regelungssysteme/13_Analyse/02_Nichtlinear
siehe: 62_Regelungssysteme/13_Analyse/02_Nichtlinear
 Übung mit Musterlösung, siehe unten bei "Übung" hier: 62_Regelungssysteme/13_Analyse/02_Nichtlinear
Übung mit Musterlösung, siehe unten bei "Übung" hier: 62_Regelungssysteme/13_Analyse/02_Nichtlinear
#9 Fr 13.06.2025
Die heutige Lehrveranstaltung findet online statt. Der Link für die Videokonferenz wurde per E-Mail verschickt.
Themen
|
1. Organisatorisches
|
2. Quiz
|
3. Übungsaufgaben
Aufgabe 1
Eine Regelstrecke habe die Übertragungsfunktion G(s)=s/(s*s+1). Sie wird mit einem Regler verbunden, der die Übertragungsfunktion R(s)=s+1 besitzt. Geben Sie nachfolgend in Scilab-Syntax des sich ergebenden Gesamtübertragungsverhaltens Q(s) des geschlossenen Regelkreises an:
Beispiel einer Übertragungsfunktion in Scilab-Syntax: G = syslin("c",[s+1],[s*s*s+2]);
s = poly(0,"s"); Q = ... (Ihre Lösung)
Code 0-21: Scilab-Code.
|
Aufgabe 2
Für das nachfolgende dynamische System soll ein Zustandsregler so ausgelegt werden, dass das Zustands-geregelte-System die Eigenwerte lambda1=-2+2i und lambda2=-2-2i besitzt.
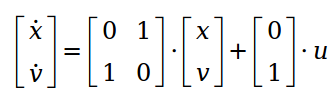
Bild 0-26: Lineares dynamisches System.
Tragen Sie nachfolgend die dann erforderlichen Werte für die Komponenten der Regelmatrix R=[r1,r2] ein:
r1 = ... r2 = ...
Code 0-22: Angabe der Regelmatrix, d.h. der Komponenten r1 und r2.
Geben Sie außerdem die veränderte Systemmatrix des Zustands-geregelten-Systems an: code Astern = Angabe der veränderten Systemmatrix A*.
Geben Sie an, ob die Regelstrecke stabil, instabil, oder grenzstabil ist:
Das System ist ...
Code 0-23: Antwort.
|
Aufgabe 3
Übertragen Sie nachfolgendes dynamische System in den Laplacebereich. Beachten Sie dabei: v = dx/dt. In dem Scilab-Skript weiter unten wird die Sprungantwort für dieses System simuliert. Ergänzen Sie darin die Übertragungsfunktion, die Sie bestimmt haben in Scilab-Syntax.
Beispiel einer Übertragungsfunktion in Scilab-Syntax: G = syslin(\"c\",[s+1],[s*s*s+2]);
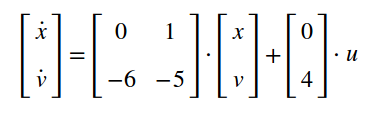
Bild 0-27: System.
s = poly(0,"s"); G = ... (Ihre Lösung) t = linspace(0.0,1.0,10); anz = size(t); u = ones(anz(1),anz(2)); ystrecke = csim(u,t,G); disp(G);
Code 0-24: Scilab-Code.
Aufgabe 4
Zur Auslegung eines PID-Reglers nach der ersten Methode von Ziegler und Nichols, wird das zu regelnde System mit einem P-Regler versehen und in den kritischen Zustand gebracht (vergl. Plot weiter unten).
Als kritische Regelverstärkung wurde Kkrit = 100 verwendet. Verwenden Sie die darunter stehende Tabelle, um die Parameter des PID-Reglers zu bestimmen.
Tragen Sie diesen Regler als Laplace-Übertragungsfunktion dann in Scilab unten ein. Hinweis: Bitte schreiben Sie keine Parameternamen hin, sondern Zahlen!
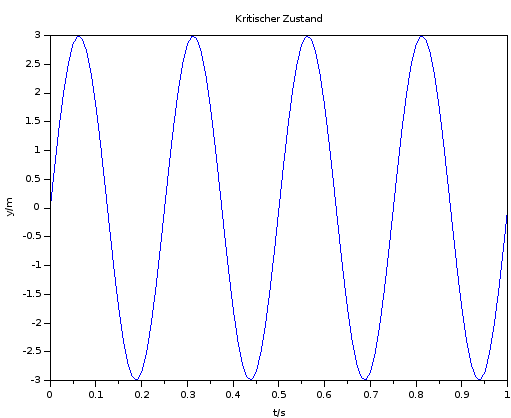
Bild 0-28: Kritischer Zustand.
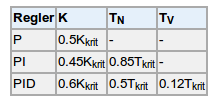
Bild 0-29: Kritischer Zustand.
s = poly(0,"s"); R = .... (Ihre Lösung) disp(R);
Code 0-25: Scilab-Code
4. Arbeitsphase
5. Besprechung der Übungsaufgaben
#10 Fr 20.06.2025
Themen
|
#11 Fr 27.06.2025
Themen
|
1. Parameteridentifikation
 50_Simulationstechnik/05_Parameterindentifikation
50_Simulationstechnik/05_Parameterindentifikation
2. Lineare Regression
 50_Simulationstechnik/05_Parameterindentifikation/01_KleinsteQuadrate/01_Linearregression
50_Simulationstechnik/05_Parameterindentifikation/01_KleinsteQuadrate/01_Linearregression
3. Die Methode der Kleinsten Quadrate
 50_Simulationstechnik/05_Parameterindentifikation/01_KleinsteQuadrate
50_Simulationstechnik/05_Parameterindentifikation/01_KleinsteQuadrate
 50_Simulationstechnik/05_Parameterindentifikation/01_KleinsteQuadrate/05_Scilab
50_Simulationstechnik/05_Parameterindentifikation/01_KleinsteQuadrate/05_Scilab
#12 Fr 04.07.2025
Klausur in elektronischer Form (E-Test) im PC-Pool, Raum D.1.02 ab 08:30Uhr.