Gradus Suivitatis
(EN google-translate)
(PL google-translate)
| coming soon :-) |
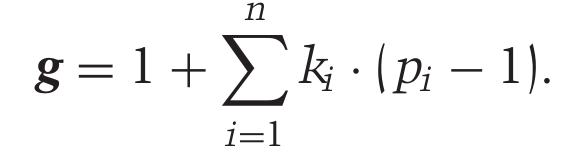
Bild 0-1: Formula for gradus suivitatis after Leonhard Euler. See also CMJ 44/1.
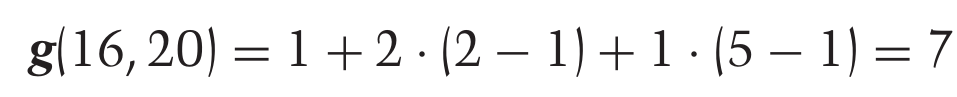
Bild 0-2: Example calculating the degree of dissonancy inbetween two numbers according to gradus suivitatis. Hint: Skip prime factors which have both numbers in common. See also CMJ 44/1.
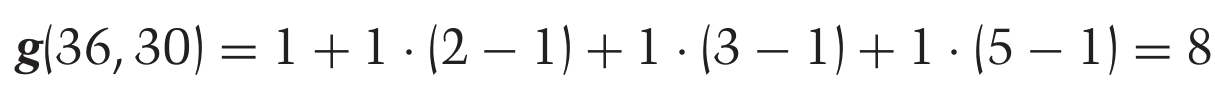
Bild 0-3: Second example.
public static int gradusSuivitatis(int a, int b)
{
int bcd = biggestCommonDivisor(a,b);
int c = (a/bcd)*(b/bcd); //rest primafactors which both a and b do not have in common.
int cc = c;
int result = 1;
for(int p=0;p<prim.length;p++)
{
if(prim[p]>c)
break;
int qq=0;
while(cc>=prim[p] && cc%prim[p]==0) {cc/=prim[p]; qq++;}
result+=(prim[p]-1)*qq;
}
return result;
}
Code 0-1: Method to calculate gradus suivitatis in Utilities.
public static int biggestCommonDivisor(int a, int b)
{
if(a==0 || b==0) return 1;
a=iabs(a);
b=iabs(b);
int x = min(a,b);
for(int i=x;i>=1;i--)
if(a%i==0 && b%i==0)
return i;
return 1;
}
Code 0-2: Helper method biggestCommonDivisor().
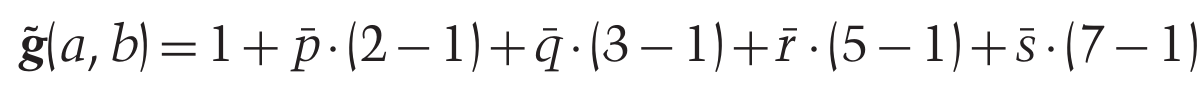
Bild 0-4: Modified version of gradus suivitatis "gradus tilde" according to the demands of AOG. See also CMJ 44/1.
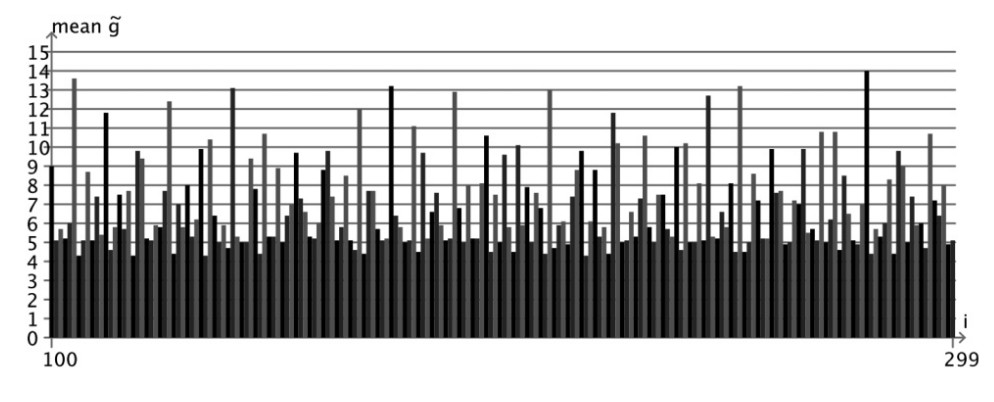
Bild 0-5: Mean g~ for each number of an excerpt of N according to 20 neighbours of each specific number. See also CMJ 44/1.