kramann.info
© Guido Kramann

HelloAOG -- Workshop for Arithmetic Operation Grammar

(EN google-translate)

(PL google-translate)

Deutsche (German) Version, siehe:

90_AOGdogma/10_HelloAOG_DE

Please take this Sketch for the workshop on June 3rd 2024:

HelloAOG2024.zip

Arithmetic Operation Grammar (AOG) was conceived as a composition method beyond the beaten track of classical theory, but also beyond established new trends [1],[2].

This method can therefore give amateurs an alternative approach to composing. Ensuring easy access to composing for non-professionals is also one of the aims of the Ubiquitous Music movement, which is why there have already been several contributions with AOG at the annual symposium on Ubiquitous Music [3],[4],[5].

The question now arises as to how such an unconventional technique, which does not follow any of the established structures, can be taught in a didactically meaningful way. This workshop takes programming in Java/Processing as its starting point. AOG structures are first presented as Java code and then replaced in a more compact way by the language tools of AOG. The familiar, from which the new is developed, is therefore not a musical theory, but a programming language. This is feasible due to the special characteristics of AOG, which are briefly presented below:

Arithmetic Operation Grammar (AOG) is a generative symbolic language for creating musical structures.
The temporal sequence of natural numbers starting at zero forms the starting point.
Varying sequences of numbers are formed by applying arithmetic operations to this temporal sequence.
For each occurring number, only the prime factors 2, 3, 5 and 7 contained therein are removed up to a limited number and their product is interpreted as a frequency in order to then play the nearest miditone as a tone, for example.
A certain proportion of the numbers therefore does not produce a playable tone. Rhythm and pitch are therefore so closely interlinked that they cannot be treated separately.
This disadvantage is accepted out of the conviction that the sequence of natural numbers and also the transformations resulting from it by means of the operations already have a structure that can be called musical in a certain sense.
In order to compensate for this disadvantage, AOG is typically implemented using software tools that provide immediate tonal feedback on the currently entered symbol sequences.
Polyphony is achieved by performing similar but not quite identical sequences of operations on the sequence of natural numbers in parallel.
The occurring frequencies do not necessarily have to be rounded to the frequency of the next mid-tone. The frequencies can also be taken unchanged, they can be given a constant factor, or/and transferred to another EMO scale with logarithmically equally distributed pitches. Microtonality is thus possible in a natural way.

References

[1] Kramann, G.: Generative Grammar Based on Arithmetic Operations for Realtime Composition. CMMR 2019, pp. 346--360.

[2] This is a preprint of "Composing by Laypeople: A Broader Perspective Provided by Arithmetic Operation Grammar". The article is published in Computer Music Journal Volume 44, No. 1, Spring of 2021, published by The MIT Press.

[3] Kramann, G.: The Lifeworld Context in Comprovizational Tools for Laypeople - A Phenomenological Approach to Explain Ease-To-Learn Aspects in User Interfaces. Ubimus 2021, https://dei.fe.up.pt/ubimus

[4] Kramann, G.: Submission of some Music Pieces for UbiMus2022 with Special Consideration of the Respective Developed User Interface for the Respective Generation Software. Ubimus 2022, ubimus2022.unespar.edu.br

[5] Kramann, G.: AOGscript - Design of a Stand-Alone Scripting Language for the Generation of Music. Ubimus 2023, ulster.ac.uk/conference/ubimus

Why the sequence of natural numbers can be said to have a musical structure?

Bild 0-1: Inner prime-factor-structure of natural numbers.

Bild 0-2: Inner prime-factor-structure of natural numbers2.

Getting Started

HelloAOG.zip -- Processing-Sketch used in the workshop, version: HelloAOGdev021 27.05.2024.

Download and install the actual version of processing for your operating system (processing.org)
Find your Sketchfolder (linux: ~/sketchfolder, windows: your_home_folder/Procesing) and unzip there HelloAOG.zip
Start Processing and find in File -> Sketchbook -> HelloAOG
Start HelloAOG, using the play-button.

Once you have successfully started the sketch, you will see and hear the following:

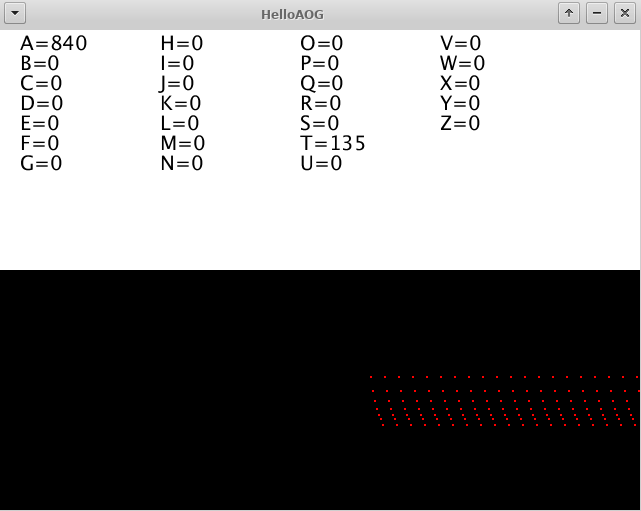
Bild 0-3: Screenshot of the running HelloAOG program.

helloaog.mp4

helloaog.ogg

The entire workshop is structured in such a way that it is usually sufficient to work in the main tab of the sketch. You do not need to pay attention to the other tabs and they will not be discussed here. In the main tab you will find predefined variables and the setup() and draw() methods. In this specific case, these are the lines of code shown below:

//version: HelloAOGdev020_workshop_BASIS 27.05.2024
int NUMBER_OF_VOICES=1;//4;
//Try to vary if stuttering in sound appears:
int SAMPLE_RATE=11025; //8000 11025 22050 44100 48000
int BUFFER_SIZE=16; //16 32 64 128 256 512
public void setup()
{
    size(640,480);
    frameRate(2);
    configure();
}
public void draw()
{
    vis.draw();
    vis.step();
    
    A=2520/(T%7+2);  
    tone1.play(A,100);
    T++;
}

Code 0-1: HelloAOG

Explanations:

First, only the last three lines of the draw() method are considered:

A=2520/(T%7+2);  
tone1.play(A,100);
T++;

Code 0-2: Last three lines of the draw() method.

2520=2*2*2*3*3*5*7
T%7+2 provides for T=0,1,2,3,...: 2,3,4,5,6,7,8,2,3,4,5,6,7,8,2,3,4,...
For T=0,1,2,3,... then is A: 1260, 840, 630, 504, 420, 360, 315, 1260, 840,...
If this cyclically repeating sequence of numbers is interpreted as frequencies, the corresponding tones have a simple frequency relationship to each other.
tone1.play(A,100); ... plays a tone with the frequency stored in the variable A and the volume 100.
The draw() method is called cyclically, because of frameRate(2); twice per second. Each time, T++ increases T by one.

More Explanations:

In this example, the occurring numbers are limited using modulo division (remainder division, operator % in Java and C++).
The use of 2520 as a number as a divisor ensures that the result corresponds to frequencies in the audible range.
By using a number as a divisor that contains only small prime factors, an important principle is immediately introduced in AOG: The frequencies played are composed only of small prime factors 2,3,5 and 7, or only numbers that satisfy this condition are considered as tones to be played.

If your computer does not display the sound correctly, you could try to solve the problem by changing the sample rate and the buffer size, see Sketch. Another possibility would be to try to give the Java process a higher priority. Finally, it would also be possible to control an external midi device instead of generating the sound directly with Java means. This would require the following (only then):

Install the library “The MidiBus” by Severin Smith within Processing (online connection required): Sketch -> Import Library -> add Library -> The MidiBus.
Go to the MIDI tab in the HelloAOG sketch and remove the comment at the very beginning /* and at the very end */.
Adjust line 9 in the CONFIGURE tab: String NAME_MIDI_DEVICE=“VirMIDI [hw:3,2,0]”; (At startup, the names of the midi devices are displayed in the terminal).
Replace line 18 in the main program (tab HelloAOG) with piano.play(0,A,40); AND IN ADDITION piano.perform();
If your Midi device is available, it should now be controlled from HelloAOG.
ALTERNATIVELY, THIS IS FOLLOWED BY THE SKETCH HelloAOGmidi, WHERE THE ADJUSTMENTS MENTIONED HERE HAVE ALREADY BEEN MADE:

HelloAOGmidi.zip -- MIDI VERSION of HelloAOG, version: HelloAOGdev021 27.05.2024.

2. Exploiting the Infinite Expanse of Natural Numbers

The preceding formula 2520/(T%7+2) ensures that only harmonically matching frequencies are played.
However, modulo division ensures that the sequence is always the same.
In the following, the maximum number of prime factors 2, 3, 5 and 7 that are present in 2520 are extracted from each number T.
This process is referred to below as REDUCTION.
This makes the complex distribution of prime factors in the sequence of natural numbers audible.
To do this, change the draw() method as follows:

public void draw()
{
    vis.draw();
    vis.step();
    
    A=2520;
    X=T;  
    B=1;
    while(A>=2 && A%2==0 && X>=2 && X%2==0) {A/=2;X/=2;B*=2;}
    while(A>=3 && A%3==0 && X>=3 && X%3==0) {A/=3;X/=3;B*=3;}
    while(A>=5 && A%5==0 && X>=5 && X%5==0) {A/=5;X/=5;B*=5;}
    while(A>=7 && A%7==0 && X>=7 && X%7==0) {A/=7;X/=7;B*=7;}

    tone1.play(A,100); //AOG-Syntax: T,2520
    //tone1.play(B,100); //AOG-Syntax: T.2520
    T++;
}

Code 0-3: Modified draw() method: Extraction of the prime factors 2,3,5,7 from T and A, as far as possible for both.

HelloAOG_2.zip -- As above modified sketch directly for download.

3. Use Of the Generative Symbolic Scripting Language Arithmetic Operation Grammar (AOG) Within Java/Processing

The two examples from 1. and 2. are now to be implemented alternatively using an interpreter from AOG.
This allows a more compact way of writing, where you can vary things more quickly.
The predefined integer variables A to Z serve as an exchange medium between Java and AOG.
Within AOG, these can be read by writing them.
If you write them as lower-case letters within AOG, they are write-accessed.

The first example, i.e. A=2520/(T%7+2) can be formulated in AOG as follows:
2520/(T%7+2)a
With the specification a at the end, what has been calculated in the line so far is transferred to A.
The conversion takes place by transferring the expression as a string to the AOG interpreter evel(...):

public void draw()
{
    vis.draw();
    vis.step();
    
    eval("2520/(T%7+2)a");
    tone1.play(A,100);
    T++;
}

Code 0-4: Example of 1. but implemented using the AOG interpreter.

HelloAOG_3.zip -- The above example is a sketch.

As already indicated by the comments in the example in 2, there are special operators to perform the reduction.
The example in 2. can therefore be implemented with AOG as follows:

public void draw()
{
    vis.draw();
    vis.step();
    
    eval("T,2520a");
    tone1.play(A,100);
    T++;
}

Code 0-5: Example in 2. implemented with AOG.

4. A More Complex Example with Four Voices Cyclically Read From File

To be able to make changes quickly, AOG can also interpret a file cyclically.
You will find the text file aogscript.txt in the project folder in the HelloAOG sketch
It has the following content:

123*(10-(T/48%10))p
T/2*P%5+1*96+(3*96)a
T/3*P%7+1*48+(3*48)*(T%2=0)*(T/2%6>0)b
T/4*P%5+1*12+(3*12)*(T%4=0)*(T/3%4>0)c
T/3*P%7+1*24+(3*24)*(T%3=0)*(T/4%3>0)d

Code 0-6: Contents of the aogscript.txt file

So that this file is interpreted cyclically by AOG, the main program can be changed in the following way:

Note: NUMBER_OF_VOICES=4; and frameRate(8);

//version: HelloAOGdev021 27.05.2024
int NUMBER_OF_VOICES=4;//4;
//Try to vary if stuttering in sound appears:
int SAMPLE_RATE=11025; //8000 11025 22050 44100 48000
int BUFFER_SIZE=16; //16 32 64 128 256 512
public void setup()
{
    size(640,480);
    frameRate(8);
    configure();
}
public void draw()
{
    vis.draw();
    vis.step();
    
    evalFile("aogscript.txt");
    
    tone1.play(A,100);
    tone2.play(B,150);
    tone3.play(C,200);
    tone4.play(D,250);
    T++;
}

Code 0-7: Modified main tab for interpreting a file.

HelloAOG_4.zip

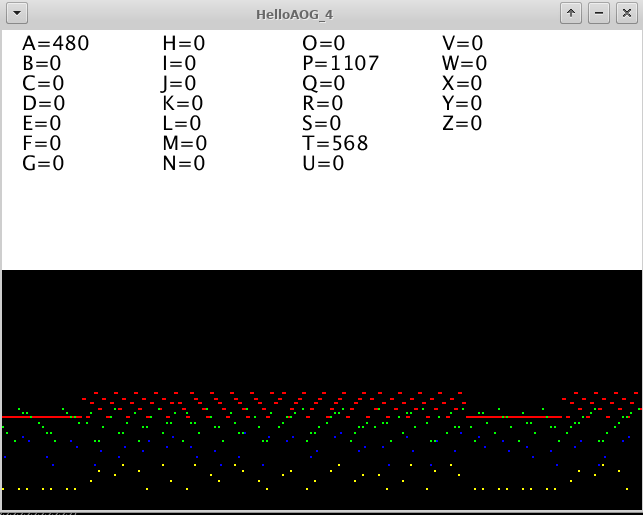
Bild 0-4: Screenshot of HelloAOG_4

Explanations

Apart from brackets (), AOG performs all operations in their natural order. For example, * is not executed before +.
123*(10-(T/48%10))p creates a sequence of multiples of 123 and stores them in P.
T/2*P%5+1*96+(3*96)a Half of T is made into a small number, which is then multiplied by 96.
T/3*P%7+1*48+(3*48)*(T%2=0)*(T/2%6>0)b One third of T is made into a small number, which is then multiplied by 48.
(T%2=0)*(T/2%6>0) are switching operations and return either 0 (false) or 1 (true).

https://youtu.be/wmYh8JLMz_c -- Realization with Disklavier.

In fact, it is difficult to fathom in retrospect what a complex script that has already been completed is doing.
Typically, such complex AOG scripts are created from a small nucleus that is gradually expanded interactively using acoustic feedback.
For example, you could start with a simple formula for just one voice, slowly expand it and create variations for other voices.
The following exercise proceeds in exactly the same way.
First, a germ cell is given and varied a little and the process is then handed over to the participants to continue individually:

5. Exercise

From a nucleus, a composition is gradually developed in several steps by implementing structural ideas as changes in the code and repeatedly checking and correcting them based on the sound feedback.

Some intermediate stages are shown below.

As an exercise, you can try to use these intermediate stages as a starting point for your own new developments.

In order to make the sound feedback as appealing as possible, a slightly extended version of the software was used, which controls a Disklavier and also offers the possibility of controlling the sustain pedal, changing the tempo and multiplying the frequencies by a percentage factor before converting them into midi tones. However, the code can also be transferred from these special features to the stand-alone software version given above. The software extension used can be found below:

HelloAOG_4_MIDI_NEU001.zip

COMPROVIZATION#1

100p    #P==Percent  frequency = 0.01*PERCENT*A..H
127s    #S==Sustain  0..127
60q     #Q==Frame Rate FPS, BPM = FPS*20
T,2520a #Extract 2,3,5,7 in 2520 which are also in T and send to A

Code 0-8: COMPROVIZATION#1

https://youtu.be/w-HKJGzeA3o -- COMPROVIZATION#1 Video

COMPROVIZATION#2

100p    #P==Percent  frequency = 0.01*PERCENT*A..H
127s    #S==Sustain  0..127
60q     #Q==Frame Rate FPS, BPM = FPS*20
7*5*9*8*(T/6%6+1)i   #I==changing base number
T,Ik #
K*(K>109)*(K<1639)*(T/12%3>0)a #set range, add breaks

Code 0-9: COMPROVIZATION#2

https://youtu.be/MtX20kGha1o -- COMPROVIZATION#2 Video

COMPROVIZATION#3

100p    #P==Percent  frequency = 0.01*PERCENT*A..H
127s    #S==Sustain  0..127
60q     #Q==Frame Rate FPS, BPM = FPS*20
7*5*9*8*(T/6%6+1)i   #I==changing base number
T%6+9000+(T/96*96)u  #Repetitions by controling time
U,Ik #
K*(K>109)*(K<1639)*(T/12%3>0)a #set range, add breaks

Code 0-10: COMPROVIZATION#3

https://youtu.be/peEL5YQJgHo -- COMPROVIZATION#3 Video

COMPROVIZATION#4

T/36%10+1*60p    #changing percentage
T/48%2*127s      #alternating sustain
60q     #Q==Frame Rate FPS, BPM = FPS*20
7*5*9*8*(T/6%6+1)i   #I==changing base number
T%6+9000+(T/96*96)u  #Repetitions by controling time
U,Ik #
K*(K>109)*(K<1639)*(T/12%3>0)a #set range, add breaks

Code 0-11: COMPROVIZATION#4

https://youtu.be/ETqAotU73bA -- COMPROVIZATION#4 Video

...und viele viele Iterationsschritte später:

COMPROVIZATION#5

T/24%10+1*(30+(T/48%5*5))p    #smaller percentage
T/48%2*60+60s    #alternating sustain
15q              #slower
7*5*9*8*(T/96%6+1)i      
T%(3+(T/3%3))+9000+(T/12*6)u     #Repetitions by controling time
T%6+9000+(T/24*12)v    #varying time structure
T%12+9000+(T/48*24)y    #varying time structure
T%24+9000+(T/96*48)z    #varying time structure
U+12w
V+24x
U/1*(U%1=0),(I*1)k   #systematically introduce variations in other voices
W/1*(W%1=0),(I*1)l
V/2*(V%2=0),(I*2)m
X/3*(X%3=0),(I*3)n

K*(K>109)*(K<1639)*(U/12%3>0)a #set range, add breaks
L*(L>109)*(L<1639)*(V/18%4>0)b 
M*(M>109)*(M<1639)*(Y/24%6>0)c 
N*(N>109)*(N<1639)*(Z/36%8>0)d

Code 0-12: COMPROVIZATION#5

https://youtu.be/-Ub04lzx7K0 -- COMPROVIZATION#5 Video

LICENSE

Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.