Mandala Music
(EN google-translate)
(PL google-translate)
TEST LATEST VERSION (Last update: 13.08.2025):
 MandalaMusicApp56_PD_KLAR_PIANO.zip -- Processing Sketch, Unpack in Processing sketch folder, restart Processing, select MandalaMusicApp036_JAVA in sketchbook.
MandalaMusicApp56_PD_KLAR_PIANO.zip -- Processing Sketch, Unpack in Processing sketch folder, restart Processing, select MandalaMusicApp036_JAVA in sketchbook.
 mandalamusicapp036_tablet_debug.apk -- Download with your Android Tablet, install and try.
mandalamusicapp036_tablet_debug.apk -- Download with your Android Tablet, install and try.
 application.linux64.zip -- stand alone PC version for Linux.
application.linux64.zip -- stand alone PC version for Linux.
 windows-amd64.zip -- stand alone PC version for windows (older version).
windows-amd64.zip -- stand alone PC version for windows (older version).
Music piece "Pan" for clarinet and piano generated with MandalaMusicApp (version 56)
Four Views of MandalaMusicApp
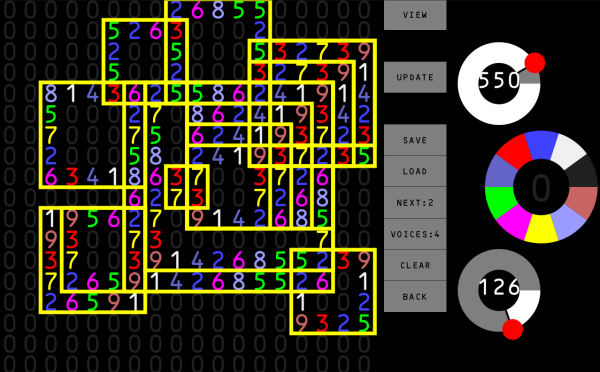
Bild 0-1: View 0: See frames consisting of numbers.

Bild 0-2: View 1: See frames consisting of symbols.
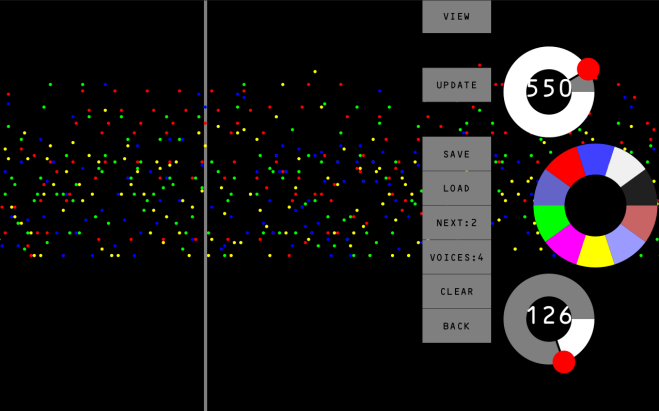
Bild 0-3: View 2: See musical score.
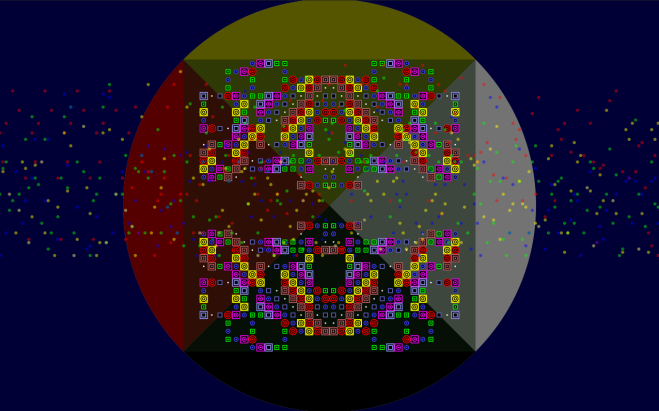
Bild 0-4: View 3: See mandala.
Some examples

Bild 0-5: Example 1.

Bild 0-6: Example 2.

Bild 0-7: Example 3.

Bild 0-8: Example 4.
From Mandala to Music / Vom Mandala zur Musik
EN: The game algorithm constantly searches for all existing cycles in real time, starting from the center of the matrix and moving outwards in a clockwise spiral. Initially, exactly one period of each sequence of digits found is displayed one below the other in the list, see figure below.
DE: Der Spielalgorithmus sucht ständig nach allen vorhandenen Zyklen in Echtzeit, wobei er in der Mitte der Matrix beginnt und sich im Uhrzeigersinn spiralförmig nach außen bewegt. Zu Beginn wird genau eine Periode jeder gefundenen Ziffernfolge von in der Liste untereinander angezeigt, siehe Abbildung unten.
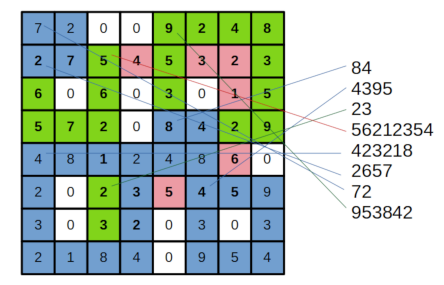
Bild 0-9: Square Frames (Mandala example).
EN: If the desired number of voices V and E is the number of entries that are to be used per voice in a time step to form a sound event, the first M=V+E-1 lines of the list are used first. The smallest common multiple K of the M lines is formed and all periods are repeated until each of the lines has the length K, see figure below.
DE: Wenn die gewünschte Anzahl der Stimmen V und E die Anzahl der Einträge ist, die pro Stimme in einem Schritt der Zeit verwendet werden sollen, um ein Klangereignis zu bilden, werden die ersten M=V+E-1 Zeilen der Liste zuerst verwendet. Aus den M Zeilen wird das kleinste gemeinsame Vielfache K gebildet und alle Perioden werden wiederholt, bis jede der Zeilen die Länge K hat, siehe Abbildung unten.

Bild 0-10: Sequences of numbers extracted from the frames.
EN: Now look at the top E numbers in each column and multiply them together. This product P, multiplied by a fixed factor F, represents the frequency frq=P*F, from which the nearest midi tone is then formed and -- if within a previously defined range -- played by the musical instrument assigned to this voice. Proceed in exactly the same way with the other voices, moving down one row in each case and then multiplying the next E values with each other from there. Moving one column to the right means calculating the notes to be played in the next time step. Once all K time steps have been processed, you move down just one row again and from there take M=V+E-1 rows from the list again and proceed in the same way, see figure below.
DE: Betrachten Sie nun die obersten E Zahlen in jeder Spalte und multiplizieren Sie sie miteinander. Dieses Produkt P, multipliziert mit einem festen Faktor F, stellt die Frequenz frq=P*F dar, aus der dann der nächste Midi-Ton gebildet wird und -- falls innerhalb eines vorher definierten Bereichs -- von dem dieser Stimme zugewiesenen Musikinstrument gespielt wird. Mit den anderen Stimmen verfahren Sie genau so , indem Sie jeweils eine Zeile nach unten gehen und von dort aus die nächsten E-Werte miteinander multiplizieren. Das Verschieben um eine Spalte nach rechts bedeutet die Berechnung der im nächsten Zeitschritt zu spielenden Noten. Wenn alle K Zeitschritte abgearbeitet sind, geht man wieder eine Zeile nach unten und nimmt von aus wieder M=V+E-1 Zeilen aus der Liste und verfährt auf die gleiche Weise, siehe Abbildung unten.

Bild 0-11: Deriving tone-frequencies from the sequences of numbers.
EN: Because the tones for the individual voices are only ever moved down one line, the change in pitch from the tone of one voice to that of the next is only determined by the division of a small number from 1 to 9 - namely the one in the line that has been left and the multiplication of a small number from 1 to 9 - namely the one in the new line that has been added. This ensures that the frequencies of the tones are in simple numerical relationships to each other.
DE: Da die Töne für die einzelnen Stimmen immer nur um eine Zeile nach unten verschoben werden, wird die Tonhöhenänderung vom Ton einer Stimme zum Ton der nächsten nur durch die Division einer kleinen Zahl von 1 bis 9 - nämlich der in der verlassenen Zeile und die Multiplikation einer kleinen Zahl von 1 bis 9 - nämlich der in der neu hinzugekommenen Zeile bestimmt. Damit ist sichergestellt, dass die Frequenzen der Töne in einfachen numerischen Beziehungen zueinander stehen.
EN: The harmonic and rhythmic structure of the resulting music also changes in small steps. This is ensured on the one hand by the cyclical character of the lines, but also by the fact that as the composition progresses after reaching time step K, it only moves down one line, see the musical result of the example described here:
DE: Die harmonische und rhythmische Struktur der entstehenden Musik verändert sich ebenfalls in kleinen Schritten. Dafür sorgt einerseits der zyklische Charakter der Zeilen, aber auch die Tatsache, dass sich die Komposition im weiteren Verlauf nach Erreichen des Zeitschritts K nur eine Zeile nach unten bewegt, siehe das musikalische Ergebnis des hier beschriebenen Beispiels:
and also a second small example in the figure below and its corresponding sonification here:
Bild 0-12: Mandala example.
Simple Example for Mandala Music

Bild 0-13: Mandala.
72009248 27545323 60603015 57208429 48124860 20235459 30320303 21840954
Code 0-1: Corresponding Matrix.
 Corresponding sonification: mandalamusic.mp3 -- This sound example was not created using the final version of the Mandala Music implementation. In particular, the velocity of the piano and the sustain pedal are not yet influenced by the progressive harmonic structure. As an example which meets these requirements, see "Fifth Example for Mandala Music" below.
Corresponding sonification: mandalamusic.mp3 -- This sound example was not created using the final version of the Mandala Music implementation. In particular, the velocity of the piano and the sustain pedal are not yet influenced by the progressive harmonic structure. As an example which meets these requirements, see "Fifth Example for Mandala Music" below.
 MandalaMusic.zip -- Processing sketch for testing Mandala Music. This is not yet the final version. In particular, the velocity of the piano and the sustain pedal are not yet influenced by the progressive harmonic structure. As an example which meets these requirements, see "Fifth Example for Mandala Music" below.
MandalaMusic.zip -- Processing sketch for testing Mandala Music. This is not yet the final version. In particular, the velocity of the piano and the sustain pedal are not yet influenced by the progressive harmonic structure. As an example which meets these requirements, see "Fifth Example for Mandala Music" below.
Key codes to work with MandalaMusic
0,1,2,3,4,5,6,7,8,9: Chose number. s: save matrix i: save matrix as an image BLANK SPACE: toggle between nomal view and mandala view
Code 0-2: Key codes to work with MandalaMusic.
Second Example for Mandala Music
Bild 0-14: Second Mandala.
523832130000000000000000 900000020000000000000000 100000060000000000000000 400000050000000000000000 500000040000000000000000 600005413900000000000000 200002090800000000000000 312383254389000000000000 000008040202000000000000 000009314501000000000000 000000020004000000000000 000000098345000000000000 000000000054923280000000 000000000002000060000000 000000000003032154560000 000000000005050030020000 000000000006040826241520 000000000008232940030030 000000000000040300040060 000000000000020200050040 000000000000065451230020 000000000000000600000030 000000000000000300000090 000000000000000251426280
Code 0-3: Corresponding Matrix.
 Corresponding sonification: mandalamusic2.mp3 -- This sound example was not created using the final version of the Mandala Music implementation. In particular, the velocity of the piano and the sustain pedal are not yet influenced by the progressive harmonic structure. As an example which meets these requirements, see "Fifth Example for Mandala Music" below.
Corresponding sonification: mandalamusic2.mp3 -- This sound example was not created using the final version of the Mandala Music implementation. In particular, the velocity of the piano and the sustain pedal are not yet influenced by the progressive harmonic structure. As an example which meets these requirements, see "Fifth Example for Mandala Music" below.
Third Example for Mandala Music
|
 Corresponding sonification: mandalamusic17.mp3
Corresponding sonification: mandalamusic17.mp3

Bild 0-15: Third Mandala
Fourth Example for Mandala Music
|
 Corresponding sonification: mandalamusic18.mp3
Corresponding sonification: mandalamusic18.mp3

Bild 0-16: Fourth Mandala
 25_UbiMus/02_Mandala_Music/mandala_mode18.png
25_UbiMus/02_Mandala_Music/mandala_mode18.png
Fifth Example for Mandala Music
|
 MandalaMusic020.zip -- Processing sketch for testing Mandala Music. In this version, the velocity and sustain pedal are controlled depending on the harmonic development of the music generated from the mandala. The current structure of the mandala is checked in real time and the generated music is immediately adapted accordingly.
MandalaMusic020.zip -- Processing sketch for testing Mandala Music. In this version, the velocity and sustain pedal are controlled depending on the harmonic development of the music generated from the mandala. The current structure of the mandala is checked in real time and the generated music is immediately adapted accordingly.
 Corresponding sonification: mandalamusic20c.mp3
Corresponding sonification: mandalamusic20c.mp3

Bild 0-17: Fifths Mandala.
 25_UbiMus/02_Mandala_Music/mandala_mode20.pdf
25_UbiMus/02_Mandala_Music/mandala_mode20.pdf